オートマタ理論

☆ オートマトン理論(Automata theory) とは、抽象的な機械やオートマトン、またそれらを用いて解くことのできる計算問題を研究する学問である。数理論理学と密接な関係を持つ理論計算機科学の理 論である。オートマトンの語源はギリシャ語の αὐτόματοςであり、「自己作用、自己意志、自己運動」を意味する。オートマトン(複数形はオートマタ)は、あらかじめ決められた一連の動作に自動 的に従う、抽象的な自走式計算装置である。有限個の状態を持つオートマトンは、有限オートマトン(FA)または有限状態機械(FSM)と呼ばれる。右の図 は有限状態機械を示しており、オートマトンの一種としてよく知られている。このオートマトンは、状態(図では丸で表現)と遷移(矢印で表現)からなる。 オートマトンは入力記号を見ると、前の状態と現在の入力記号を引数とする遷移関数に従って、別の状態への遷移(またはジャンプ)を行う。 オートマトン理論は、形式言語理論と密接に関連している。この文脈では、オートマトンは無限である可能性のある形式言語の有限表現として用いられる。オー トマトンはしばしば、オートマトンの主要なクラス間の入れ子関係を記述するチョムスキー階層にあるように、認識できる形式言語のクラスによって分類され る。オートマトンは、計算理論、コンパイラ構築、人工知能、構文解析、形式検証において重要な役割を果たしている。
| History The theory of abstract automata was developed in the mid-20th century in connection with finite automata.[1] Automata theory was initially considered a branch of mathematical systems theory, studying the behavior of discrete-parameter systems. Early work in automata theory differed from previous work on systems by using abstract algebra to describe information systems rather than differential calculus to describe material systems.[2] The theory of the finite-state transducer was developed under different names by different research communities.[3] The earlier concept of Turing machine was also included in the discipline along with new forms of infinite-state automata, such as pushdown automata. 1956 saw the publication of Automata Studies, which collected work by scientists including Claude Shannon, W. Ross Ashby, John von Neumann, Marvin Minsky, Edward F. Moore, and Stephen Cole Kleene.[4] With the publication of this volume, "automata theory emerged as a relatively autonomous discipline".[5] The book included Kleene's description of the set of regular events, or regular languages, and a relatively stable measure of complexity in Turing machine programs by Shannon.[6] In the same year, Noam Chomsky described the Chomsky hierarchy, a correspondence between automata and formal grammars,[7] and Ross Ashby published An Introduction to Cybernetics, an accessible textbook explaining automata and information using basic set theory. The study of linear bounded automata led to the Myhill–Nerode theorem,[8] which gives a necessary and sufficient condition for a formal language to be regular, and an exact count of the number of states in a minimal machine for the language. The pumping lemma for regular languages, also useful in regularity proofs, was proven in this period by Michael O. Rabin and Dana Scott, along with the computational equivalence of deterministic and nondeterministic finite automata.[9] In the 1960s, a body of algebraic results known as "structure theory" or "algebraic decomposition theory" emerged, which dealt with the realization of sequential machines from smaller machines by interconnection.[10] While any finite automaton can be simulated using a universal gate set, this requires that the simulating circuit contain loops of arbitrary complexity. Structure theory deals with the "loop-free" realizability of machines.[5] The theory of computational complexity also took shape in the 1960s.[11][12] By the end of the decade, automata theory came to be seen as "the pure mathematics of computer science".[5] |
オートマトンの歴史 抽象オートマトンの理論は、20世紀半ばに有限オートマトンに関連して開発された[1]。オートマトン理論は当初、離散パラメータ系の振る舞いを研究する 数学システム論の一分野と考えられていた。オートマトン理論の初期の研究は、物質的なシステムを記述する微分積分学ではなく、情報システムを記述する抽象 代数学を使用することによって、システムに関する以前の研究とは異なっていた[2]。 有限状態トランスデューサの理論は、異なる研究コミュニティによって異なる名前で開発された[3]。チューリング機械の以前の概念は、プッシュダウンオー トマトンなどの無限状態オートマトンの新しい形式とともに、この分野に含まれていた。 1956年、クロード・シャノン、W.ロス・アシュビー、ジョン・フォン・ノイマン、マービン・ミンスキー、エドワード・F.ムーア、スティーブン・コー ル・クリーンを含む科学者の研究を集めた『オートマトン研究』が出版された。 [同年、ノーム・チョムスキーはオートマトンと形式文法の対応関係であるチョムスキー階層を説明し[7]、ロス・アシュビーは基本的な集合論を使ってオー トマトンと情報を説明するわかりやすい教科書『サイバネティクス入門』を出版した。 線形有界オートマトンの研究は、形式言語が正則であるための必要十分条件と、その言語の最小機械における状態数の正確なカウントを与えるMyhill- Nerode定理[8]につながった。正則性の証明にも有用な正則言語のポンピングのレンマは、決定論的有限オートマトンと非決定論的有限オートマトンの 計算上の等価性とともに、マイケル・O・ラビン(Michael O. Rabin)とダナ・スコット(Dana Scott)によってこの時期に証明された[9]。 1960年代には、「構造理論」または「代数的分解理論」として知られる代数的結果が出現し、相互接続によってより小さなマシンから逐次マシンを実現する ことを扱った[10]。あらゆる有限オートマトンはユニバーサルゲート集合を使ってシミュレートできるが、そのためにはシミュレート回路が任意の複雑さの ループを含む必要がある。構造論は機械の「ループのない」実現可能性を扱っている[5]。計算複雑さの理論も1960年代に形成された[11][12]。 |
| Automata What follows is a general definition of an automaton, which restricts a broader definition of a system to one viewed as acting in discrete time-steps, with its state behavior and outputs defined at each step by unchanging functions of only its state and input.[5] Informal description An automaton runs when it is given some sequence of inputs in discrete (individual) time steps (or just steps). An automaton processes one input picked from a set of symbols or letters, which is called an input alphabet. The symbols received by the automaton as input at any step are a sequence of symbols called words. An automaton has a set of states. At each moment during a run of the automaton, the automaton is in one of its states. When the automaton receives new input, it moves to another state (or transitions) based on a transition function that takes the previous state and current input symbol as parameters. At the same time, another function called the output function produces symbols from the output alphabet, also according to the previous state and current input symbol. The automaton reads the symbols of the input word and transitions between states until the word is read completely, if it is finite in length, at which point the automaton halts. A state at which the automaton halts is called the final state. To investigate the possible state/input/output sequences in an automaton using formal language theory, a machine can be assigned a starting state and a set of accepting states. Then, depending on whether a run starting from the starting state ends in an accepting state, the automaton can be said to accept or reject an input sequence. The set of all the words accepted by an automaton is called the language recognized by the automaton. A familiar example of a machine recognizing a language is an electronic lock, which accepts or rejects attempts to enter the correct code. |
オートマトン 以下はオートマトンの一般的な定義である。オートマトンは、より広範なシステムの定義を、離散的な時間ステップで動作し、各ステップで状態と入力のみの不変関数によって定義された状態動作と出力を持つものと見なすことに限定する[5]。 非公式な記述 オートマトンは、離散的な(個々の)時間ステップ(または単にステップ)で入力のシーケンスが与えられたときに実行される。オートマトンは、入力アルファ ベットと呼ばれる記号または文字の集合から選んだ1つの入力を処理する。オートマトンが任意のステップで入力として受け取る記号は、単語と呼ばれる記号列 である。オートマトンは状態の集合を持つ。オートマトンの実行中の各瞬間において、オートマトンはいずれかの状態にある。オートマトンが新しい入力を受け 取ると、前の状態と現在の入力記号をパラメータとする遷移関数に基づいて、オートマトンは別の状態に移る(あるいは遷移する)。同時に、出力関数と呼ばれ る別の関数が、同じく前の状態と現在の入力記号に従って、出力アルファベットから記号を生成する。オートマトンは入力ワードの記号を読み、ワードの長さが 有限であれば、完全に読み終わるまで状態間を遷移し、その時点で停止する。オートマトンが停止する状態を最終状態と呼ぶ。 形式言語理論を用いてオートマトンにおける可能な状態/入出力シーケンスを調べるには、機械に開始状態と受け入れ状態のセットを割り当てる。そして、開始 状態から始まる実行が受け入れ状態で終わるかどうかに応じて、オートマトンは入力シーケンスを受け入れるか拒否すると言うことができる。オートマトンが受 け入れるすべての単語の集合を、オートマトンが認識する言語と呼ぶ。言語を認識する機械の身近な例としては、電子錠がある。 |
 Recognizable languages The recognizable languages are the set of languages that are recognized by some automaton. For finite automata the recognizable languages are regular languages. For different types of automata, the recognizable languages are different. |
認識可能な言語 認識可能な言語とは、あるオートマトンが認識する言語の集合である。有限オートマトンでは、認識可能な言語は正則言語である。異なるタイプのオートマトンでは、認識可能な言語は異なる。 |
| Variant definitions of automata Automata are defined to study useful machines under mathematical formalism. So the definition of an automaton is open to variations according to the "real world machine" that we want to model using the automaton. People have studied many variations of automata. The following are some popular variations in the definition of different components of automata. Input Finite input: An automaton that accepts only finite sequences of symbols. The above introductory definition only encompasses finite words. Infinite input: An automaton that accepts infinite words (ω-words). Such automata are called ω-automata. Tree input: The input may be a tree of symbols instead of sequence of symbols. In this case after reading each symbol, the automaton reads all the successor symbols in the input tree. It is said that the automaton makes one copy of itself for each successor and each such copy starts running on one of the successor symbols from the state according to the transition relation of the automaton. Such an automaton is called a tree automaton. Infinite tree input : The two extensions above can be combined, so the automaton reads a tree structure with (in)finite branches. Such an automaton is called an infinite tree automaton. States Single state: An automaton with one state, also called a combinational circuit, performs a transformation which may implement combinational logic.[10] Finite states: An automaton that contains only a finite number of states. Infinite states: An automaton that may not have a finite number of states, or even a countable number of states. Different kinds of abstract memory may be used to give such machines finite descriptions. Stack memory: An automaton may also contain some extra memory in the form of a stack in which symbols can be pushed and popped. This kind of automaton is called a pushdown automaton. Queue memory: An automaton may have memory in the form of a queue. Such a machine is called queue machine and is Turing-complete. Tape memory: The inputs and outputs of automata are often described as input and output tapes. Some machines have additional working tapes, including the Turing machine, linear bounded automaton, and log-space transducer. Transition function Deterministic: For a given current state and an input symbol, if an automaton can only jump to one and only one state then it is a deterministic automaton. Nondeterministic: An automaton that, after reading an input symbol, may jump into any of a number of states, as licensed by its transition relation. The term transition function is replaced by transition relation: The automaton non-deterministically decides to jump into one of the allowed choices. Such automata are called nondeterministic automata. Alternation: This idea is quite similar to tree automata but orthogonal. The automaton may run its multiple copies on the same next read symbol. Such automata are called alternating automata. The acceptance condition must be satisfied on all runs of such copies to accept the input. Two-wayness: Automata may read their input from left to right, or they may be allowed to move back-and-forth on the input, in a way similar to a Turing machine. Automata which can move back-and-forth on the input are called two-way finite automata. Acceptance condition Acceptance of finite words: Same as described in the informal definition above. Acceptance of infinite words: an ω-automaton cannot have final states, as infinite words never terminate. Rather, acceptance of the word is decided by looking at the infinite sequence of visited states during the run. Probabilistic acceptance: An automaton need not strictly accept or reject an input. It may accept the input with some probability between zero and one. For example, quantum finite automata, geometric automata and metric automata have probabilistic acceptance. Different combinations of the above variations produce many classes of automata. Automata theory is a subject matter that studies properties of various types of automata. For example, the following questions are studied about a given type of automata. Which class of formal languages is recognizable by some type of automata? (Recognizable languages) Are certain automata closed under union, intersection, or complementation of formal languages? (Closure properties) How expressive is a type of automata in terms of recognizing a class of formal languages? And, their relative expressive power? (Language hierarchy) Automata theory also studies the existence or nonexistence of any effective algorithms to solve problems similar to the following list: Does an automaton accept at least one input word? (Emptiness checking) Is it possible to transform a given non-deterministic automaton into a deterministic automaton without changing the language recognized? (Determinization) For a given formal language, what is the smallest automaton that recognizes it? (Minimization) |
オートマトンの定義 オートマトンは、数学的形式論の下で有用な機械を研究するために定義される。だから、オートマトンの定義は、そのオートマトンを使ってモデル化したい「実 世界の機械」に応じて変幻自在である。オートマトンには多くのバリエーションがある。以下は、オートマトンのさまざまな構成要素の定義における、よく使わ れるバリエーションである。 入力 有限入力: 有限の記号列のみを受け入れるオートマトン。上記の入門的な定義は、有限の単語のみを包含する。 無限入力: 無限の単語(ω-words)を受け入れるオートマトン。このようなオートマトンは ω-automata と呼ばれる。 木入力: 入力は記号列ではなく、記号の木であってもよい。この場合、オートマトンは各記号を読み取った後、入力木に含まれるすべての後続記号を読み取る。このオー トマトンは、各継続記号に対して自身のコピーを1つ作成し、各コピーは、オートマトンの遷移関係に従って、状態から後継記号の1つに対して実行を開始す る。このようなオートマトンを木オートマトンと呼ぶ。 無限木入力:上の2つの拡張を組み合わせると、オートマトンは(中略)有限の枝を持つ木構造を読み取る。このようなオートマトンを無限木オートマトンと呼ぶ。 状態 単一状態: 状態を1つ持つオートマトンは組み合わせ回路とも呼ばれ、組み合わせ論理を実装するパフォーマティビティを実行する[10]。 有限状態: 有限状態:有限個の状態しか持たないオートマトン。 無限状態: オートマトンは有限個の状態、あるいは数えられる数の状態を持たない。このような機械に有限の記述を与えるために、さまざまな種類の抽象記憶が使われる。 スタックメモリ: オートマトンは、記号をプッシュしたりポップしたりすることができるスタックという形の余分なメモリを含むこともある。この種のオートマトンはプッシュダウン・オートマトンと呼ばれる。 キュー・メモリー: オートマトンは待ち行列の形のメモリを持つこともある。このような機械は待ち行列機械と呼ばれ、チューリング完全である。 テープ記憶: オートマトンの入力と出力は、しばしば入力テープと出力テープとして表現される。チューリング機械、線形有界オートマトン、対数空間変換器など、追加の作業テープを持つ機械もある。 遷移関数 決定論的: 与えられた現在の状態と入力記号に対して、オートマトンが1つの状態にしかジャンプできない場合、それは決定論的オートマトンである。 非決定論的: 非決定論的オートマトン: 入力記号を読み込んだ後、遷移関係によって許可されたいくつかの状態のいずれかにジャンプできるオートマトン。遷移関数は遷移関係に置き換えられる: オートマトンは非決定的に、許容される選択肢の1つにジャンプすることを決定する。このようなオートマトンを非決定性オートマトンと呼ぶ。 交互作用: この考え方はツリー・オートマトンに似ているが、直交する。オートマトンは、同じ次の読み出しシンボルに対して複数のコピーを実行することができる。この ようなオートマトンを交替オートマトンと呼ぶ。入力を受け入れるためには、このようなコピーのすべての実行で受け入れ条件が満たされなければならない。 双方向性: オートマトンは、入力を左から右に読むこともできるし、チューリング機械に似た方法で、入力上を行ったり来たりすることもできる。入力上を行ったり来たりできるオートマトンは、双方向有限オートマトンと呼ばれる。 受け入れ条件 有限語の受け入れ: 上記の非公式な定義で説明したのと同じである。 無限語の受け入れ: ω-オートマトンは最終状態を持つことができない。むしろ、単語の受け入れは、実行中に訪れる状態の無限列を見て決定される。 確率的受け入れ: オートマトンは入力を厳密に受け入れたり拒否したりする必要はない。オートマトンは、ゼロから1の間の確率で入力を受け入れることができる。例えば、量子有限オートマトン、幾何オートマトン、計量オートマトンなどは、確率的受容を持つ。 これらの組み合わせによって、多くのオートマトン・クラスが生まれる。 オートマトン理論は、様々な種類のオートマトンの性質を研究する主題である。例えば、ある種類のオートマトンについて以下のような問題が研究される。 ある種類のオートマトンによって認識可能な形式言語のクラスはどれか?(認識可能な言語) あるオートマトンは、形式言語の和、交、補のいずれに対しても閉じているか?(閉包の性質) ある種類のオートマトンは、あるクラスの形式言語を認識する上で、どの程度の表現力を持つか?また、その相対的な表現力は?(言語階層) オートマトン理論では、次のような問題を解くための効果的なアルゴリズムが存在するかどうかも研究している: オートマトンは少なくとも一つの入力語を受け入れるか? 与えられた非決定論的オートマトンを、認識される言語を変えることなく決定論的オートマトンに変換することは可能か?(決定化) ある形式言語について、それを認識する最小のオートマトンは何か?(最小化) |
| Applications Each model in automata theory plays important roles in several applied areas. Finite automata are used in text processing, compilers, and hardware design. Context-free grammar (CFGs) are used in programming languages and artificial intelligence. Originally, CFGs were used in the study of human languages. Cellular automata are used in the field of artificial life, the most famous example being John Conway's Game of Life. Some other examples which could be explained using automata theory in biology include mollusk and pine cone growth and pigmentation patterns. Going further, a theory suggesting that the whole universe is computed by some sort of a discrete automaton, is advocated by some scientists. The idea originated in the work of Konrad Zuse, and was popularized in America by Edward Fredkin. Automata also appear in the theory of finite fields: the set of irreducible polynomials that can be written as composition of degree two polynomials is in fact a regular language.[15] Another problem for which automata can be used is the induction of regular languages. |
応用分野 オートマトン理論の各モデルは、いくつかの応用分野で重要な役割を果たしている。有限オートマトンは、テキスト処理、コンパイラ、ハードウェア設計に使わ れている。文脈自由文法(CFG)は、プログラミング言語や人工知能に使われている。もともとCFGは人間の言語の研究に使われていた。セル・オートマト ンは人工生命の分野で使われており、最も有名な例はジョン・コンウェイの「ゲーム・オブ・ライフ」である。生物学でオートマトン理論を使って説明できる他 の例としては、軟体動物や松ぼっくりの成長パターンや色素形成パターンなどがある。さらに進んで、宇宙全体がある種の離散オートマトンによって計算されて いるという理論が、一部の科学者によって提唱されている。この考えはコンラート・ズースの研究に端を発し、エドワード・フレドキンがアメリカで広めた。 オートマトンは有限体論にも登場する。次数2の多項式の合成として書ける既約多項式の集合は、実は正則言語である。 |
| Automata simulators Automata simulators are pedagogical tools used to teach, learn and research automata theory. An automata simulator takes as input the description of an automaton and then simulates its working for an arbitrary input string. The description of the automaton can be entered in several ways. An automaton can be defined in a symbolic language or its specification may be entered in a predesigned form or its transition diagram may be drawn by clicking and dragging the mouse. Well known automata simulators include Turing's World, JFLAP, VAS, TAGS and SimStudio.[16] |
オートマトンシミュレータ オートマトン・シミュレータは、オートマトン理論の教育、学習、研究に使われる教育ツールである。オートマトン・シミュレータは、オートマトンの記述を入 力とし、任意の入力文字列に対するオートマトンの動作をシミュレートする。オートマトンの記述はいくつかの方法で入力できる。オートマトンは記号言語で定 義することもできるし、その仕様をあらかじめデザインされた形式で入力することも、マウスをクリックしてドラッグすることで遷移図を描くこともできる。よ く知られたオートマトン・シミュレーターには、チューリングの世界、JFLAP、VAS、TAGS、SimStudioがある[16]。 |
| Category-theoretic models One can define several distinct categories of automata[17] following the automata classification into different types described in the previous section. The mathematical category of deterministic automata, sequential machines or sequential automata, and Turing machines with automata homomorphisms defining the arrows between automata is a Cartesian closed category,[18] it has both categorical limits and colimits. An automata homomorphism maps a quintuple of an automaton Ai onto the quintuple of another automaton Aj. Automata homomorphisms can also be considered as automata transformations or as semigroup homomorphisms, when the state space, S, of the automaton is defined as a semigroup Sg. Monoids are also considered as a suitable setting for automata in monoidal categories.[19][20][21] Categories of variable automata One could also define a variable automaton, in the sense of Norbert Wiener in his book on The Human Use of Human Beings via the endomorphisms {\displaystyle A_{i}\to A_{i}}. Then one can show that such variable automata homomorphisms form a mathematical group. In the case of non-deterministic, or other complex kinds of automata, the latter set of endomorphisms may become, however, a variable automaton groupoid. Therefore, in the most general case, categories of variable automata of any kind are categories of groupoids or groupoid categories. Moreover, the category of reversible automata is then a 2-category, and also a subcategory of the 2-category of groupoids, or the groupoid category. |
カテゴリー理論的モデル 前節で述べたオートマトンのタイプ分類に従って、オートマトンのいくつかの異なるカテゴリーを定義することができる[17]。決定論的オートマトン、逐次 機械または逐次オートマトン、オートマトン間の矢印を定義するオートマトン同型性を持つチューリング機械の数学的カテゴリは直交閉カテゴリであり [18]、カテゴリ極限とコリミットの両方を持つ。オートマトン同型は、オートマトンAiの五重項を別のオートマトンAjの五重項に写像する。オートマト ンの状態空間Sが半群Sgとして定義されている場合、オートマトンの同型性はオートマトンの変換、または半群の同型性としても考えることができる。モノイ ドはまた、モノイドカテゴリのオートマトンのための適切な設定として考えられている[19][20][21]。 可変オートマトンのカテゴリー また、ノルベルト・ウィーナー(Norbert Wiener)の著書『The Human Use of Human Beings』における意味での可変オートマトンを定義することもできる。 {displaystyle A_{i}to A_{i}}である。 そして、このような可変オートマトンの同型性が数学的なグループを形成することを示すことができる。非決定論的なオートマトン、あるいは他の複雑なオート マトンの場合、後者の同型の集合は、しかし、可変オートマトンの群体になる可能性がある。したがって、最も一般的なケースでは、あらゆる種類の可変オート マトンのカテゴリは、群体のカテゴリまたは群体のカテゴリである。さらに、可逆オートマトンの範疇は、2範疇であり、また、群体の2範疇、または群体範疇 の部分範疇である。 |
| https://en.wikipedia.org/wiki/Automata_theory |
|
★オー トマトン理論(オートマタはオートマトンの複数形表現)
| Automata theory
is the study of abstract machines and automata, as well as the
computational problems that can be solved using them. It is a theory in
theoretical computer science with close connections to mathematical
logic. The word automata comes from the Greek word αὐτόματος, which
means "self-acting, self-willed, self-moving". An automaton (automata
in plural) is an abstract self-propelled computing device which follows
a predetermined sequence of operations automatically. An automaton with
a finite number of states is called a finite automaton (FA) or
finite-state machine (FSM). The figure on the right illustrates a
finite-state machine, which is a well-known type of automaton. This
automaton consists of states (represented in the figure by circles) and
transitions (represented by arrows). As the automaton sees a symbol of
input, it makes a transition (or jump) to another state, according to
its transition function, which takes the previous state and current
input symbol as its arguments. Automata theory is closely related to formal language theory. In this context, automata are used as finite representations of formal languages that may be infinite. Automata are often classified by the class of formal languages they can recognize, as in the Chomsky hierarchy, which describes a nesting relationship between major classes of automata. Automata play a major role in the theory of computation, compiler construction, artificial intelligence, parsing and formal verification. |
オートマトン理論とは、抽象的な機械やオートマトン、またそれらを用い
て解くことのできる計算問題を研究する学問である。数理論理学と密接な関係を持つ理論計算機科学の理論である。オートマトンの語源はギリシャ語の
αὐτόματοςであり、「自己作用、自己意志、自己運動」を意味する。オートマトン(複数形はオートマタ)は、あらかじめ決められた一連の動作に自動
的に従う、抽象的な自走式計算装置である。有限個の状態を持つオートマトンは、有限オートマトン(FA)または有限状態機械(FSM)と呼ばれる。右の図
は有限状態機械を示しており、オートマトンの一種としてよく知られている。このオートマトンは、状態(図では丸で表現)と遷移(矢印で表現)からなる。
オートマトンは入力記号を見ると、前の状態と現在の入力記号を引数とする遷移関数に従って、別の状態への遷移(またはジャンプ)を行う。 オートマトン理論は、形式言語理論と密接に関連している。この文脈では、オートマトンは無限である可能性のある形式言語の有限表現として用いられる。オー トマトンはしばしば、オートマトンの主要なクラス間の入れ子関係を記述するチョムスキー階層にあるように、認識できる形式言語のクラスによって分類され る。オートマトンは、計算理論、コンパイラ構築、人工知能、構文解析、形式検証において重要な役割を果たしている。 |
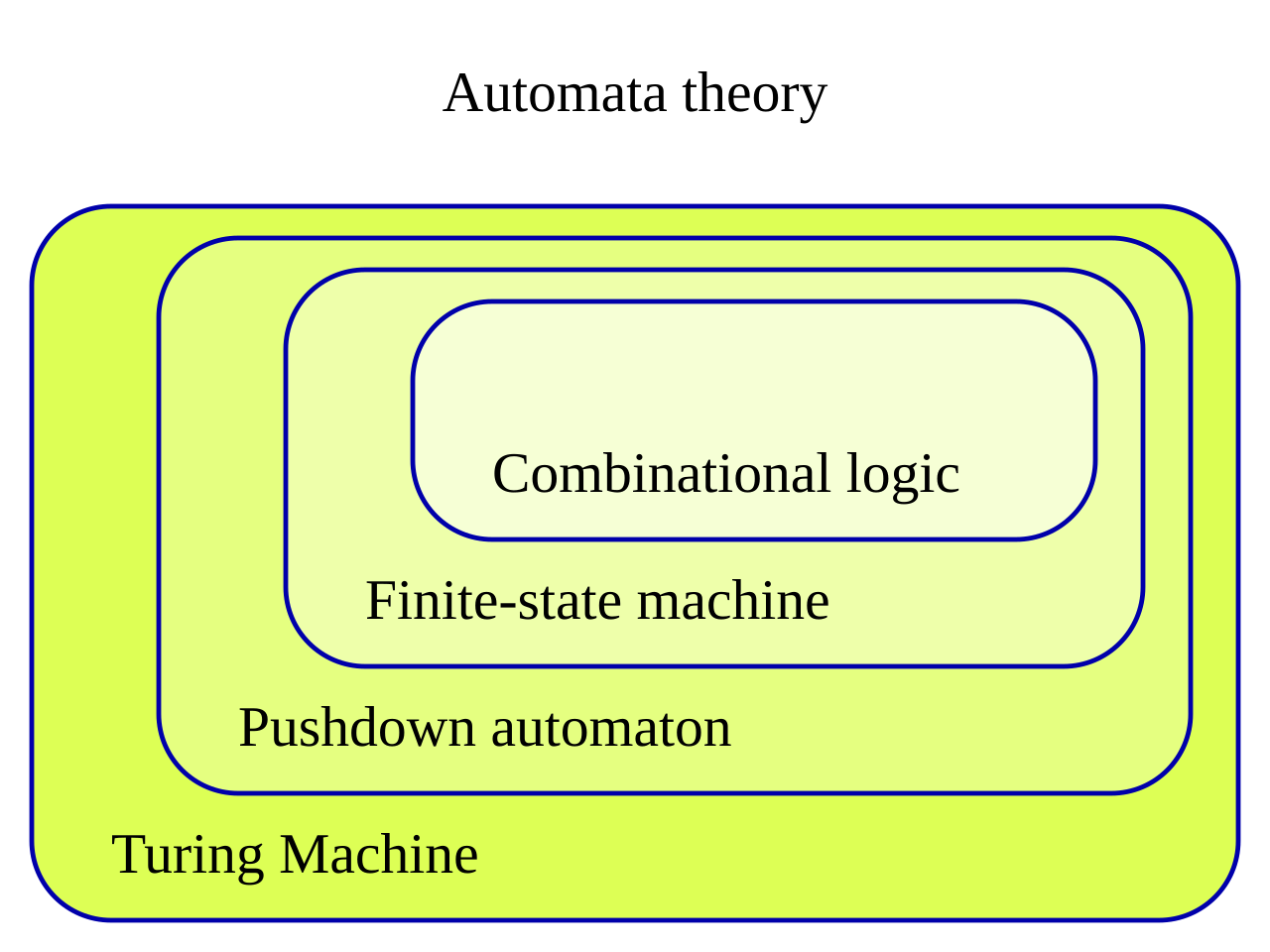
| Classes of automata (Clicking on each layer gets an article on that subject)  |
オートマトンのクラス (各層をクリックすると、そのテーマに関する記事が表示される)  |
| In automata theory,
combinational logic (also referred to as time-independent logic[1]) is
a type of digital logic that is implemented by Boolean circuits, where
the output is a pure function of the present input only. This is in
contrast to sequential logic, in which the output depends not only on
the present input but also on the history of the input. In other words,
sequential logic has memory while combinational logic does not. Combinational logic is used in computer circuits to perform Boolean algebra on input signals and on stored data. Practical computer circuits normally contain a mixture of combinational and sequential logic. For example, the part of an arithmetic logic unit, or ALU, that does mathematical calculations is constructed using combinational logic. Other circuits used in computers, such as half adders, full adders, half subtractors, full subtractors, multiplexers, demultiplexers, encoders and decoders are also made by using combinational logic. Practical design of combinational logic systems may require consideration of the finite time required for practical logical elements to react to changes in their inputs. Where an output is the result of the combination of several different paths with differing numbers of switching elements, the output may momentarily change state before settling at the final state, as the changes propagate along different paths. [2] |
オートマトン理論では、組み合わせ論理(時間非依存論理[1]とも呼ば
れる)はブール回路で実装されるデジタル論理の一種であり、出力は現在の入力のみの純粋関数である。これは、出力が現在の入力だけでなく、入力の履歴にも
依存する逐次論理とは対照的である。言い換えれば、逐次論理にはメモリがあるが、組合せ論理にはない。 組合せ論理は、コンピュータ回路において、入力信号および記憶されたデータに対してブール代数を実行するために使用される。実用的なコンピュータ回路に は、通常、組合せ論理と逐次論理が混在している。例えば、算術論理演算装置(ALU)のうち、数学的計算を行う部分は組合せ論理で構成されている。その 他、半加算器、全加算器、半減算器、全減算器、マルチプレクサ、デマルチプレクサ、エンコーダ、デコーダなど、コンピュータで使われる回路も組み合わせ論 理で作られている。 組合せ論理システムの実用的な設計には、実用的な論理素子が入力の変化に反応するのに必要な有限時間を考慮する必要があるかもしれない。出力が、スイッチ ング素子の数が異なる複数の異なる経路の組み合わせの結果である場合、出力は、変化が異なる経路に沿って伝播するため、最終的な状態に落ち着く前に瞬間的 に状態が変化する可能性がある。[2] |
| A finite-state machine (FSM) or
finite-state automaton (FSA, plural: automata), finite automaton, or
simply a state machine, is a mathematical model of computation. It is
an abstract machine that can be in exactly one of a finite number of
states at any given time. The FSM can change from one state to another
in response to some inputs; the change from one state to another is
called a transition.[1] An FSM is defined by a list of its states, its
initial state, and the inputs that trigger each transition.
Finite-state machines are of two types—deterministic finite-state
machines and non-deterministic finite-state machines.[2] For any
non-deterministic finite-state machine, an equivalent deterministic one
can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are: vending machines, which dispense products when the proper combination of coins is deposited; elevators, whose sequence of stops is determined by the floors requested by riders; traffic lights, which change sequence when cars are waiting; combination locks, which require the input of a sequence of numbers in the proper order. The finite-state machine has less computational power than some other models of computation such as the Turing machine.[3] The computational power distinction means there are computational tasks that a Turing machine can do but an FSM cannot. This is because an FSM's memory is limited by the number of states it has. A finite-state machine has the same computational power as a Turing machine that is restricted such that its head may only perform "read" operations, and always has to move from left to right. FSMs are studied in the more general field of automata theory. |
有限状態機械(FSM)または有限状態オートマトン(FSA、複数形は
オートマトン)、有限オートマトン、または単に状態機械は、計算の数学的モデルである。FSMは、任意の時点で有限個の状態のうちの1つになることができ
る抽象的な機械である。FSMは、ある入力に応答して、ある状態から別の状態に変化することができる。ある状態から別の状態への変化は遷移と呼ばれる。有
限状態マシンには、決定論的有限状態マシンと非決定論的有限状態マシンの2種類がある。 ステートマシンのパフォーマティビティは、現代社会の多くの装置で観察することができ、それらは、提示されたイベントのシーケンスに応じて、予め決められ た一連の動作を実行する。簡単な例としては、適切な硬貨の組み合わせが投入されると商品が払い出される自動販売機、乗車客が要求した階によって停止順序が 決まるエレベーター、車が待機していると順序が変わる信号機、適切な順序の数字列の入力を必要とするコンビネーション・ロックなどがある。 有限状態機械は、チューリング機械などの他の計算モデルよりも計算能力が低い[3]。計算能力の違いは、チューリング機械にはできるが、FSMにはできな い計算タスクがあることを意味する。これは、FSMのメモリが状態の数によって制限されるためである。有限状態機械は、チューリング機械と同じ計算能力を 持つが、その頭部は「読み取り」操作しか行えず、常に左から右に移動しなければならないという制約がある。FSMは、より一般的なオートマトン理論の分野 で研究されている。 |
| In the theory of computation, a
branch of theoretical computer science, a pushdown automaton (PDA) is a
type of automaton that employs a stack. Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines (see below). Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages, with the former often used in parser design. The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata.[1] A nested stack automaton allows full access, and also allows stacked values to be entire sub-stacks rather than just single finite symbols. |
理論計算機科学の一分野である計算理論において、プッシュダウン・オー
トマトン(PDA)はスタックを用いたオートマトンの一種である。 プッシュダウン・オートマトンは、機械が何を計算できるかという理論に使われる。有限状態機械よりは高性能だが、チューリング機械(後述)よりは性能が劣 る。決定論的プッシュダウン・オートマトンはすべての決定論的文脈自由言語を認識することができ、非決定論的プッシュダウン・オートマトンはすべての文脈 自由言語を認識することができる。 プッシュダウン」とは、スタックが、カフェテリアのトレー・ディスペンサーのように「押し下げられる」とみなすことができることを意味する。対照的に、ス タック・オートマトンは、より深い要素へのアクセスと操作を可能にする。スタック・オートマトンは、プッシュダウン・オートマトンよりも厳密に大きな言語 集合を認識することができる[1]。ネストされたスタック・オートマトンは、完全なアクセスを可能にし、また、スタックされた値を単一の有限記号ではな く、サブスタック全体にすることができる。 |
| A Turing machine is a
mathematical model of computation describing an abstract machine[1]
that manipulates symbols on a strip of tape according to a table of
rules.[2] Despite the model's simplicity, it is capable of implementing
any computer algorithm.[3] The machine operates on an infinite[4] memory tape divided into discrete cells,[5] each of which can hold a single symbol drawn from a finite set of symbols called the alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right,[6] or halts the computation. The choice of which replacement symbol to write, which direction to move the head, and whether to halt is based on a finite table that specifies what to do for each combination of the current state and the symbol that is read. Like a real computer program, it is possible for a Turing machine to go into an infinite loop which will never halt. The Turing machine was invented in 1936 by Alan Turing,[7][8] who called it an "a-machine" (automatic machine).[9] It was Turing's doctoral advisor, Alonzo Church, who later coined the term "Turing machine" in a review.[10] With this model, Turing was able to answer two questions in the negative: Does a machine exist that can determine whether any arbitrary machine on its tape is "circular" (e.g., freezes, or fails to continue its computational task)? Does a machine exist that can determine whether any arbitrary machine on its tape ever prints a given symbol?[11][12] Thus by providing a mathematical description of a very simple device capable of arbitrary computations, he was able to prove properties of computation in general—and in particular, the uncomputability of the Entscheidungsproblem ('decision problem').[13] Turing machines proved the existence of fundamental limitations on the power of mechanical computation.[14] While they can express arbitrary computations, their minimalist design makes them too slow for computation in practice: real-world computers are based on different designs that, unlike Turing machines, use random-access memory. Turing completeness is the ability for a computational model or a system of instructions to simulate a Turing machine. A programming language that is Turing complete is theoretically capable of expressing all tasks accomplishable by computers; nearly all programming languages are Turing complete if the limitations of finite memory are ignored. |
チューリング機械は、抽象的な機械[1]を記述する計算の数学的モデル
であり、規則表に従ってテープ片上の記号を操作する[2]。このモデルは単純であるにもかかわらず、あらゆるコンピュータアルゴリズムを実装することがで
きる[3]。 マシンは、離散的なセル[5]に分割された無限[4]のメモリテープ上で動作し、各セルは、マシンのアルファベットと呼ばれる記号の有限集合から引き出さ れた単一の記号を保持することができる。マシンの動作のどの時点でも、これらのセルの1つの上に配置される「ヘッド」と、有限の状態セットから選択される 「状態」を持つ。動作の各段階で、ヘッドはそのセルのシンボルを読み取る。次に、その記号とマシン自身の現在の状態に基づいて、マシンは同じセルに記号を 書き込み、ヘッドを左または右に1ステップ動かすか[6]、計算を停止する。どの置換記号を書き込むか、ヘッドをどの方向に動かすか、そして停止す るかどうかの選択は、現在の状態と読み込まれた記号の組み合わせごとに何をす べきか規定した有限表に基づいている。実際のコンピュータ・プログラムのように、チューリング・マシンが無限ループに入ることは可能であり、決して停止す ることはない。 チューリング機械は1936年にアラン・チューリングによって発明され[7][8]、彼はこれを「a-machine」(自動機械)と呼んだ[9]。 チューリングの博士課程の指導教官であったアロンゾ・チャーチが、後にレビューの中で「チューリング機械」という言葉を作った[10]: テープ上の任意の機械が「循環」(例えば、フリーズしたり、計算タスクを継続できなかったり)するかどうかを決定できる機械は存在するか? テープ上の任意の機械が、与えられた記号を印刷したことがあるかどうかを決定できる機械は存在するか[11][12]。 こうしてチューリングは、任意の計算が可能な非常に単純な装置の数学的記述を提供することによって、一般的な計算の特性、特に Entscheidungsproblem(「決定問題」)の計算不可能性を証明することができた[13]。 チューリング機械は任意の計算を表現することができるが、そのミニマリスト的な設計のため、実際の計算には遅すぎる。 チューリング完全性とは、計算モデルや命令体系がチューリング機械をシミュレートする能力のことである。チューリング完全性を持つプログラミング言語は、 理論的にはコンピュータが達成可能なすべてのタスクを表現できる。有限メモリの制約を無視すれば、ほぼすべてのプログラミング言語はチューリング完全性を 持つ。 |
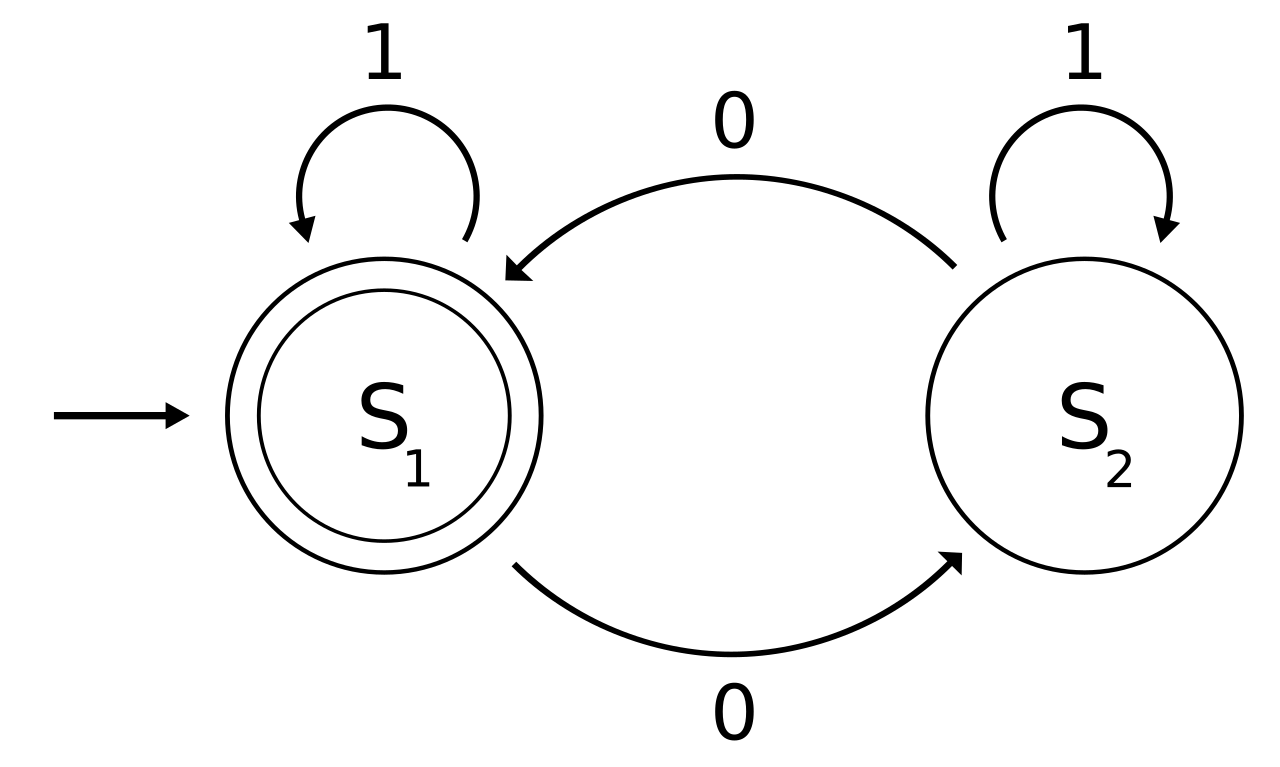 The automaton described by this state diagram starts in state S1, and changes states following the arrows marked 0 or 1 according to the input symbols as they arrive. The double circle marks S1 as an accepting state. Since all paths from S1 to itself contain an even number of arrows marked 0, this automaton accepts strings containing even numbers of 0s. |
 この状態図で記述されるオートマトンは状態S1から始まり、入力記号の到着に従って0または1と書かれた矢印に従って状態を変化させる。二重丸はS1が受 け入れ状態であることを示す。S1からそれ自身へのすべての経路は偶数の0と書かれた矢印を含むので、このオートマトンは偶数の0を含む文字列を受け入れ る。 |
| https://en.wikipedia.org/wiki/Automata_theory |
+++++
++++++++
リ ンク
文 献
そ の他の情報
Copyleft, CC, Mitzub'ixi Quq Chi'j, 1996-2099
☆
 ☆
☆