チョムスキー階層
Chomsky hierarchy
☆ 形式言語理論、コンピュータサイエンス、言語学の分野におけるチョムスキー階層(Chomsky-Schützenberger hierarchy[1]と呼ばれることもある)は、形式文法のクラスの包含階層である。形式文法とは、ある言語の語彙(またはアルファベット)から、そ の言語の構文に従って妥当な文字列を形成する方法を記述するものである。言語学者のノーム・チョムスキーは、次第に複雑な言語を生成できる4つの異なるク ラスの形式文法が存在すると理論化した。各クラスはまた、すべての劣ったクラス(セット包括的)の言語を完全に生成することができる。
| The Chomsky hierarchy
(infrequently referred to as the Chomsky–Schützenberger hierarchy[1])
in the fields of formal language theory, computer science, and
linguistics, is a containment hierarchy of classes of formal grammars.
A formal grammar describes how to form strings from a language's
vocabulary (or alphabet) that are valid according to the language's
syntax. The linguist Noam Chomsky theorized that four different classes
of formal grammars existed that could generate increasingly complex
languages. Each class can also completely generate the language of all
inferior classes (set inclusive). |
形
式言語理論、コンピュータサイエンス、言語学の分野におけるチョムスキー階層(Chomsky-Schützenberger
hierarchy[1]と呼ばれることもある)は、形式文法のクラスの包含階層である。形式文法とは、ある言語の語彙(またはアルファベット)から、そ
の言語の構文に従って妥当な文字列を形成する方法を記述するものである。言語学者のノーム・チョムスキーは、次第に複雑な言語を生成できる4つの異なるク
ラスの形式文法が存在すると理論化した。各クラスはまた、すべての劣ったクラス(セット包括的)の言語を完全に生成することができる。 |
| History The general idea of a hierarchy of grammars was first described by Noam Chomsky in "Three models for the description of language".[2] Marcel-Paul Schützenberger also played a role in the development of the theory of formal languages; the paper "The algebraic theory of context free languages"[3] describes the modern hierarchy, including context-free grammars.[1] Independently, alongside linguists, mathematicians were developing models of computation (via automata). Parsing a sentence in a language is similar to computation, and the grammars described by Chomsky proved to both resemble and be equivalent in computational power to various machine models.[4] |
歴史 文法の階層構造という一般的な考え方は、ノーム・チョムスキーが "Three models for the description of language"[2]の中で初めて記述したものである。マルセル=ポール・シュッツェンベルガーもまた、形式言語理論の発展に一役買った。"The algebraic theory of context free languages"[3]という論文には、文脈自由文法を含む現代の階層構造が記述されている[1]。 言語学者とは別に、数学者も(オートマトンによる)計算モデルを開発していた。チョムスキーによって記述された文法は、様々な機械モデルと類似しており、計算能力も同等であることが証明された[4]。 |
| The hierarchy The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, the type of automaton that recognizes it, and the form its rules must have. The classes are defined by the constraints on the productions rules. 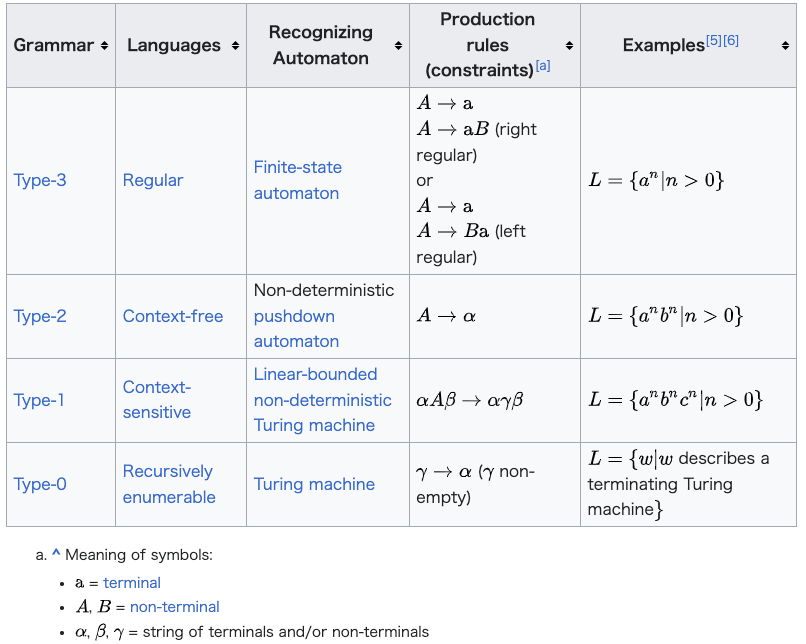 Note that the set of grammars corresponding to recursive languages is not a member of this hierarchy; these would be properly between Type-0 and Type-1. Every regular language is context-free, every context-free language is context-sensitive, every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages that are not context-sensitive, context-sensitive languages that are not context-free and context-free languages that are not regular.[7] Regular (Type-3) grammars Main article: Regular grammar Type-3 grammars generate the regular languages. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal, possibly followed by a single nonterminal, in which case the grammar is right regular. Alternatively, all the rules can have their right-hand sides consist of a single terminal, possibly preceded by a single nonterminal (left regular). These generate the same languages. However, if left-regular rules and right-regular rules are combined, the language need no longer be regular. The rule � → �{\displaystyle S\rightarrow \varepsilon } is also allowed here if � {\displaystyle S} does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite-state automaton. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.  |
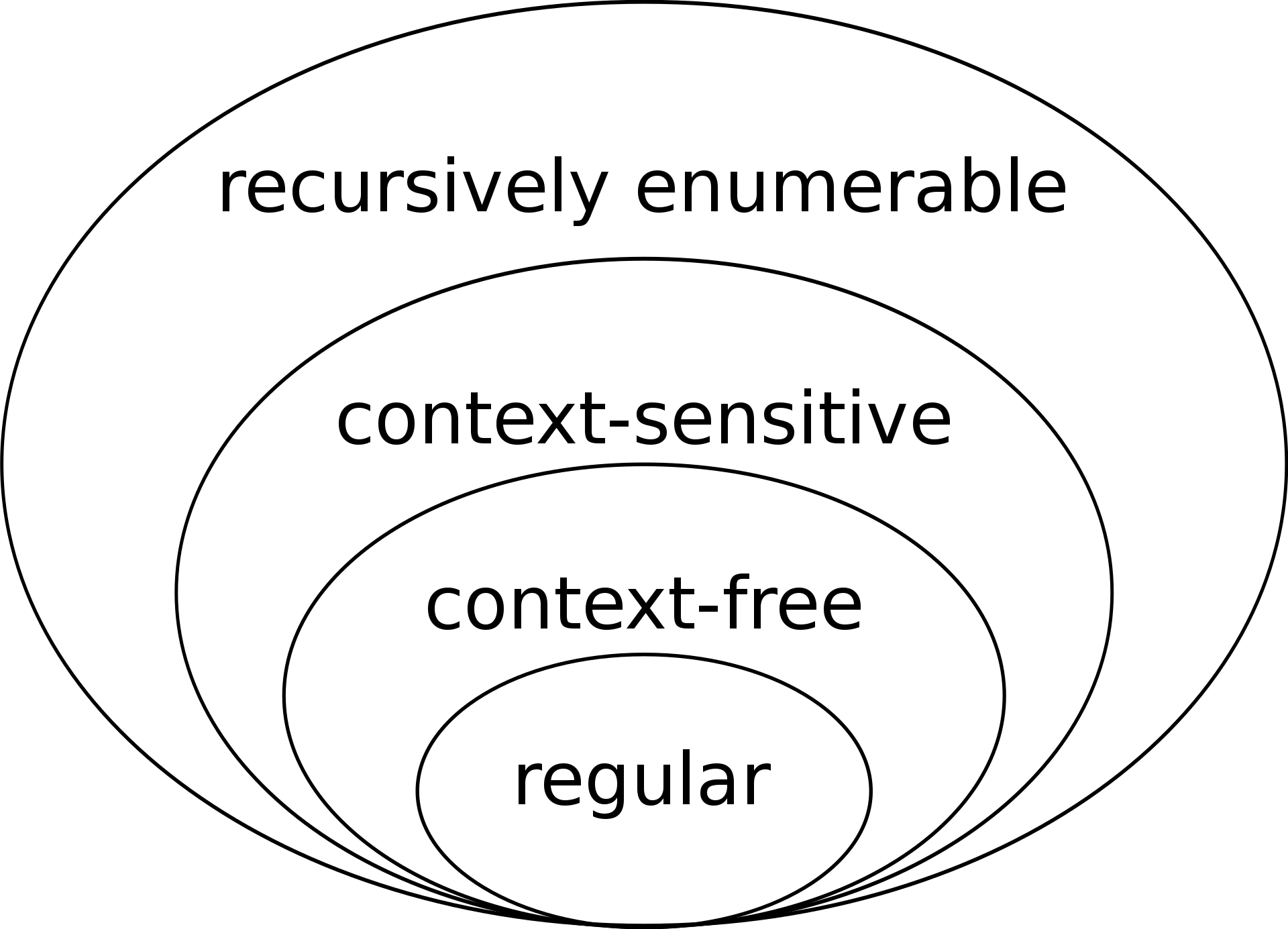
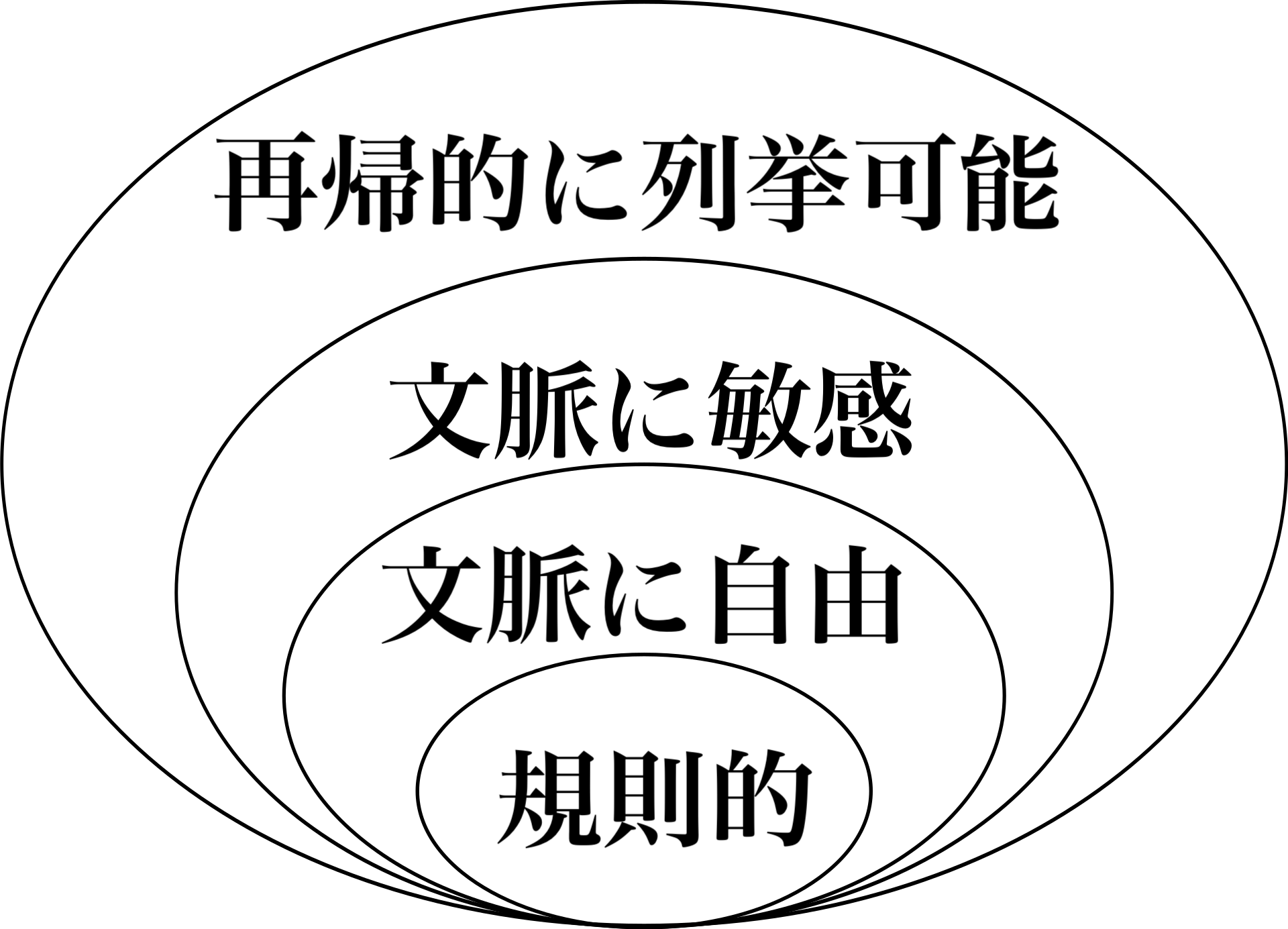
階層構造 次の表は、チョムスキーの4種類の文法、それが生成する言語のクラス、それを認識するオートマトンの種類、およびその規則が持つべき形式をまとめたものである。クラスは生成規則の制約によって定義される。  再帰的言語に対応する文法の集合はこの階層には含まれない。 すべての正規言語は文脈自由であり、すべての文脈自由言語は文脈依存であり、すべての文脈依存言語は再帰的であり、すべての再帰的言語は再帰的に列挙可能 である。これらはすべて適切な包含であり、文脈依存でない再帰的に列挙可能な言語、文脈自由でない文脈依存な言語、規則的でない文脈自由な言語が存在する ことを意味する[7]。 正規(Type-3)文法 主な記事 正規文法 Type-3文法は正規言語を生成する。このような文法は、左辺が1つの非終端、右辺が1つの終端、場合によってはそれに続く1つの非終端からなる規則に 限定される。あるいは、すべての規則の右辺を1つの終端から構成し、場合によってはその前に1つの非終端を置くこともできる(左規則)。これらは同じ言語 を生成する。しかし、左規則と右規則が組み合わされた場合、言語はもはや規則的である必要はない。規則 � → という規則も許される。 � がどの規則の右辺にも現れない場合、�→�{displaystyle S}も許される。これらの言語は、まさに有限状態オートマトンが決定できるすべての言語である。さらに、この形式言語のファミリーは正規表現によって得る ことができる。正規表現は、検索パターンやプログラミング言語の字句構造を定義するためによく使われる。 |
| Recursively enumerable (Type-0) grammars Main article: Unrestricted grammar Type-0 grammars include all formal grammars. There are no constraints on the productions rules. They generate exactly all languages that can be recognized by a Turing machine, thus any language that is possible to be generated can be generated by a Type-0 grammar.[8] These languages are also known as the recursively enumerable or Turing-recognizable languages.[8] Note that this is different from the recursive languages, which can be decided by an always-halting Turing machine. |
再帰的に列挙可能な(Type-0)文法 主な記事 制限のない文法 Type-0文法にはすべての形式文法が含まれる。生成規則には制約がない。このため、生成可能な言語はすべてType-0文法によって生成することができる[8]。これらの言語は再帰的に列挙可能な言語またはチューリング認識可能な言語としても知られている[8]。 |
| Chomsky normal form |
|
| https://en.wikipedia.org/wiki/Chomsky_hierarchy |
|
リ ンク
文 献
そ の他の情報
Copyleft, CC, Mitzub'ixi Quq Chi'j, 1996-2099
☆
 ☆
☆