パララックス
Parallax; 視差
☆視 差とは、2つの異なる視線に沿っ て見た物体の見かけ上の位置のずれまたは差異であり、2つの視線間の傾斜角または半傾斜角によって測定される。[1][2] 遠近法により、遠くの物体よりも近くの物体の方が視差が大きくなるため、視差は距離を測定するために使用することができる。
| Parallax
is a displacement or difference in the apparent position of an object
viewed along two different lines of sight and is measured by the angle
or half-angle of inclination between those two lines.[1][2] Due to
foreshortening, nearby objects show a larger parallax than farther
objects, so parallax can be used to determine distances. To measure large distances, such as the distance of a planet or a star from Earth, astronomers use the principle of parallax. Here, the term parallax is the semi-angle of inclination between two sight-lines to the star, as observed when Earth is on opposite sides of the Sun in its orbit.[a] These distances form the lowest rung of what is called "the cosmic distance ladder", the first in a succession of methods by which astronomers determine the distances to celestial objects, serving as a basis for other distance measurements in astronomy forming the higher rungs of the ladder. Parallax also affects optical instruments such as rifle scopes, binoculars, microscopes, and twin-lens reflex cameras that view objects from slightly different angles. Many animals, along with humans, have two eyes with overlapping visual fields that use parallax to gain depth perception; this process is known as stereopsis. In computer vision the effect is used for computer stereo vision, and there is a device called a parallax rangefinder that uses it to find the range, and in some variations also altitude to a target. A simple everyday example of parallax can be seen in the dashboards of motor vehicles that use a needle-style mechanical speedometer. When viewed from directly in front, the speed may show exactly 60, but when viewed from the passenger seat, the needle may appear to show a slightly different speed due to the angle of viewing combined with the displacement of the needle from the plane of the numerical dial. |
視差とは、2つの異なる視線に沿っ
て見た物体の見かけ上の位置のずれまたは差異であり、2つの視線間の傾斜角または半傾斜角によって測定される。[1][2]
遠近法により、遠くの物体よりも近くの物体の方が視差が大きくなるため、視差は距離を測定するために使用することができる。 地球から惑星や恒星までの距離など、大きな距離を測定するために、天文学者は視差の原理を使用する。ここでいう視差とは、地球が太陽の周りを回る軌道上で 地球が太陽の反対側に位置しているときに観測される、星までの2つの視線間の傾斜角の半分の角度である。[a] これらの距離は、「宇宙の距離はしご」と呼ばれるものの最下層を形成しており、天文学者が天体までの距離を測定する方法の最初の段階であり、はしごの上層 に位置する天文学における他の距離測定の基礎となる。 視差は、ライフルスコープ、双眼鏡、顕微鏡、二眼レフカメラなど、対象をわずかに異なる角度から見る光学機器にも影響を与える。人間をはじめ多くの動物 は、視野が重なり合う2つの目を持っており、視差を利用して奥行きを認識している。このプロセスは立体視として知られている。コンピュータビジョンでは、 この効果はコンピュータステレオビジョンに使用され、視差を利用して距離を測定する視差測距装置と呼ばれる装置がある。また、いくつかのバリエーションで は、対象物の高度も測定できる。 視差の日常的な簡単な例としては、針式の機械式速度計を使用している自動車のダッシュボードが挙げられる。正面から見ると、速度は正確に60と表示されて いるように見えるが、助手席から見ると、針の角度と数字のダイヤル面からの針のずれが組み合わさって、速度がわずかに異なって表示されているように見える ことがある。 |
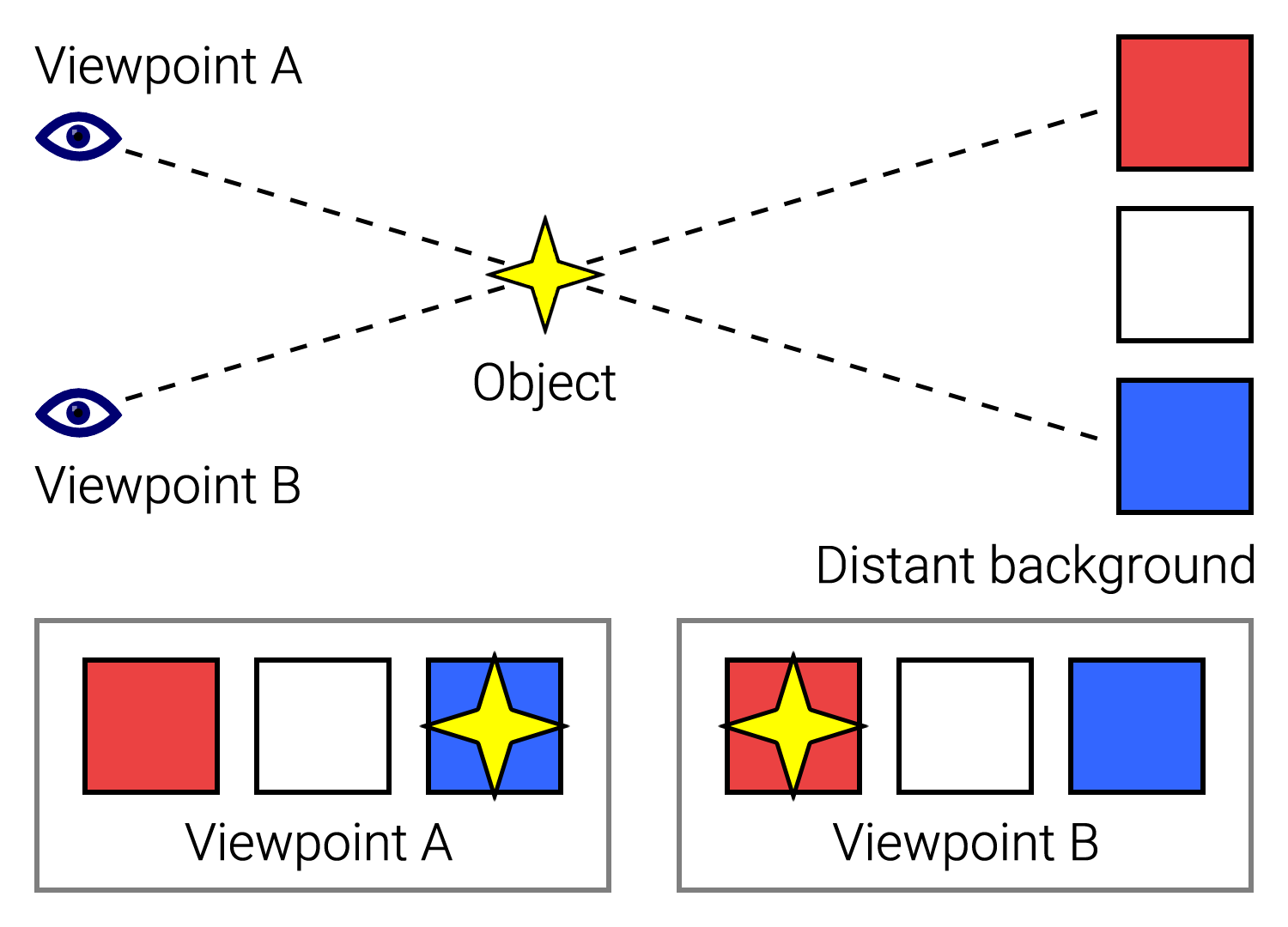
 A simplified illustration of the parallax of an object against a distant background due to a perspective shift. When viewed from "Viewpoint A", the object appears to be in front of the blue square. When the viewpoint is changed to "Viewpoint B", the object appears to have moved in front of the red square. |
 遠景の背景に対して、視点移動により物体がずれて見える視差の簡易図解。視点A」から見ると、物体は青い四角形の手前に見える。視点が「視点B」に変わる と、物体は赤い四角形の手前に移動したように見える。 |
 This animation is an example of parallax. As the viewpoint moves side to side, the objects in the distance appear to move more slowly than the objects close to the camera. In this case, the white cube in front appears to move faster than the green cube in the middle of the far background. |
 このアニメーションは視差の例である。視点が左右に移動すると、遠くにある物体はカメラに近い物体よりもゆっくりと動いているように見える。この場合、手 前の白い立方体は、遠くの背景の中央にある緑色の立方体よりも速く動いているように見える。 |
| Visual perception Main articles: stereopsis, depth perception, binocular vision, and binocular disparity  In this photograph, the Sun is visible above the top of the streetlight. In the reflection on the water, the Sun appears in line with the streetlight because the virtual image is formed from a different viewing position. Because the eyes of humans and other animals are in different positions on the head, they present different views simultaneously. This is the basis of stereopsis, the process by which the brain exploits the parallax due to the different views from the eye to gain depth perception and estimate distances to objects.[3] Animals also use motion parallax, in which the animals (or just the head) move to gain different viewpoints. For example, pigeons (whose eyes do not have overlapping fields of view and thus cannot use stereopsis) bob their heads up and down to see depth.[4] The motion parallax is exploited also in wiggle stereoscopy, computer graphics that provide depth cues through viewpoint-shifting animation rather than through binocular vision. |
視覚知覚 主な記事:立体視、奥行き知覚、両眼視、両眼視差  この写真では、街灯の上方に太陽が見える。水面に映った太陽は、街灯と一直線上に並んで見えるが、これは仮想像が異なる視点から形成されるためである。 人間や他の動物は、頭部の異なる位置に目があるため、同時に異なる視界を得ている。これが立体視の基礎であり、脳が異なる視界による視差を活用して奥行き 知覚や物体までの距離を推定するプロセスである。 動物は、動物(または頭部のみ)を動かして異なる視点を得る動き視差も利用している。例えば、ハト(両眼の視野が重ならないため立体視ができない)は、頭 を上下に動かして奥行きを認識している。[4] 動き視差は、両眼視ではなく視点移動のアニメーションによって奥行きの手がかりを提供するコンピュータグラフィックスである「ウィグル立体視」でも利用さ れている。 |
Distance measurement Parallax theory for finding naval distances Parallax arises due to a change in viewpoint occurring due to the motion of the observer, of the observed, or both. What is essential is relative motion. By observing parallax, measuring angles, and using geometry, one can determine distance. Distance measurement by parallax is a special case of the principle of triangulation, which states that one can solve for all the sides and angles in a network of triangles if, in addition to all the angles in the network, the length of at least one side has been measured. Thus, the careful measurement of the length of one baseline can fix the scale of an entire triangulation network. In parallax, the triangle is extremely long and narrow, and by measuring both its shortest side (the motion of the observer) and the small top angle (always less than 1 arcsecond,[5] leaving the other two close to 90 degrees), the length of the long sides (in practice considered to be equal) can be determined. In astronomy, assuming the angle is small, the distance to a star (measured in parsecs) is the reciprocal of the parallax (measured in arcseconds): 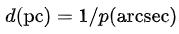 On Earth, a coincidence rangefinder or parallax rangefinder can be used to find distance to a target. In surveying, the problem of resection explores angular measurements from a known baseline for determining an unknown point's coordinates. |
距離測定 海軍の距離を測定するための視差理論 視差は、観察者、観察対象、あるいはその両方の運動によって生じる視点の変化によって生じる。本質的なのは相対運動である。視差を観察し、角度を測定し、 幾何学を使用することで、距離を測定することができる。 視差による距離測定は、三角測量の原理の特別なケースであり、三角形のネットワークのすべての角度に加えて、少なくとも1辺の長さが測定されていれば、三 角形のネットワークのすべての辺と角度を求めることができるというものである。したがって、1つの基線の長さを注意深く測定すれば、三角測量ネットワーク 全体の縮尺を確定することができる。視差では、三角形は極端に細長い。その最短辺(観測者の動き)と小さな頂角(常に1秒未満[5]で、他の2辺は90度 に近い)の両方を測定することで、長い辺の長さ(実際には等しいとみなされる)を決定することができる。 天文学では、その角度が小さいと仮定すると、恒星までの距離(パーセクで測定)は視差(秒角で測定)の逆数となる。 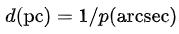 地球上で、偶然の一致による測距儀または視差測距儀を使用して、対象までの距離を測定することができる。測量では、 resection(後退測量)の問題は、未知の点の座標を決定するために、既知の基線からの角度測定を調査する。 |
| Astronomy This section is an excerpt from Parallax in astronomy.[edit] 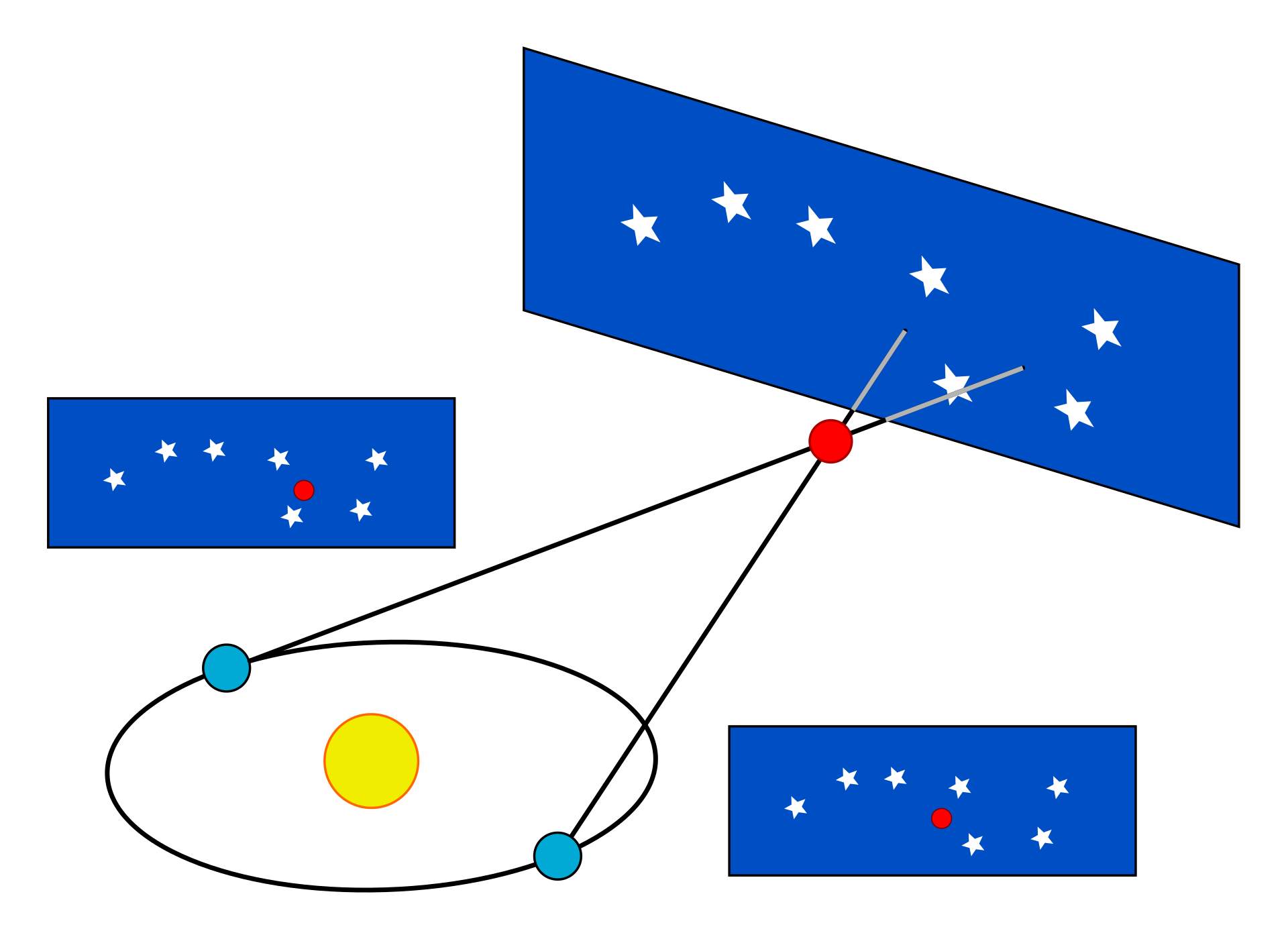 Stellar parallax motion from annual parallax. Half the apex angle is the parallax angle. 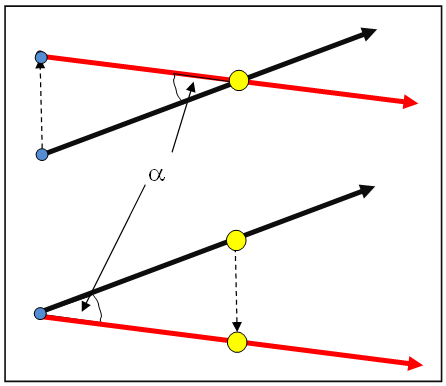 Parallax is an angle subtended by a line on a point. In the upper diagram, the Earth in its orbit sweeps the parallax angle subtended on the Sun. The lower diagram shows an equal angle swept by the Sun in a geostatic model. A similar diagram can be drawn for a star except that the angle of parallax would be minuscule. The most important fundamental distance measurements in astronomy come from trigonometric parallax, as applied in the stellar parallax method. As the Earth orbits the Sun, the position of nearby stars will appear to shift slightly against the more distant background. These shifts are angles in an isosceles triangle, with 2 AU (the distance between the extreme positions of Earth's orbit around the Sun) making the base leg of the triangle and the distance to the star being the long equal-length legs. The amount of shift is quite small, even for the nearest stars, measuring 1 arcsecond for an object at 1 parsec's distance (3.26 light-years), and thereafter decreasing in angular amount as the distance increases. Astronomers usually express distances in units of parsecs (parallax arcseconds); light-years are used in popular media. Because parallax becomes smaller for a greater stellar distance, useful distances can be measured only for stars which are near enough to have a parallax larger than a few times the precision of the measurement. In the 1990s, for example, the Hipparcos mission obtained parallaxes for over a hundred thousand stars with a precision of about a milliarcsecond,[7] providing useful distances for stars out to a few hundred parsecs. The Hubble Space Telescope's Wide Field Camera 3 has the potential to provide a precision of 20 to 40 microarcseconds, enabling reliable distance measurements up to 5,000 parsecs (16,000 ly) for small numbers of stars.[8][9] The Gaia space mission provided similarly accurate distances to most stars brighter than 15th magnitude.[10] Distances can be measured within 10% as far as the Galactic Center, about 30,000 light years away. Stars have a velocity relative to the Sun that causes proper motion (transverse across the sky) and radial velocity (motion toward or away from the Sun). The former is determined by plotting the changing position of the stars over many years, while the latter comes from measuring the Doppler shift of the star's spectrum caused by motion along the line of sight. For a group of stars with the same spectral class and a similar magnitude range, a mean parallax can be derived from statistical analysis of the proper motions relative to their radial velocities. This statistical parallax method is useful for measuring the distances of bright stars beyond 50 parsecs and giant variable stars, including Cepheids and the RR Lyrae variables.[11] 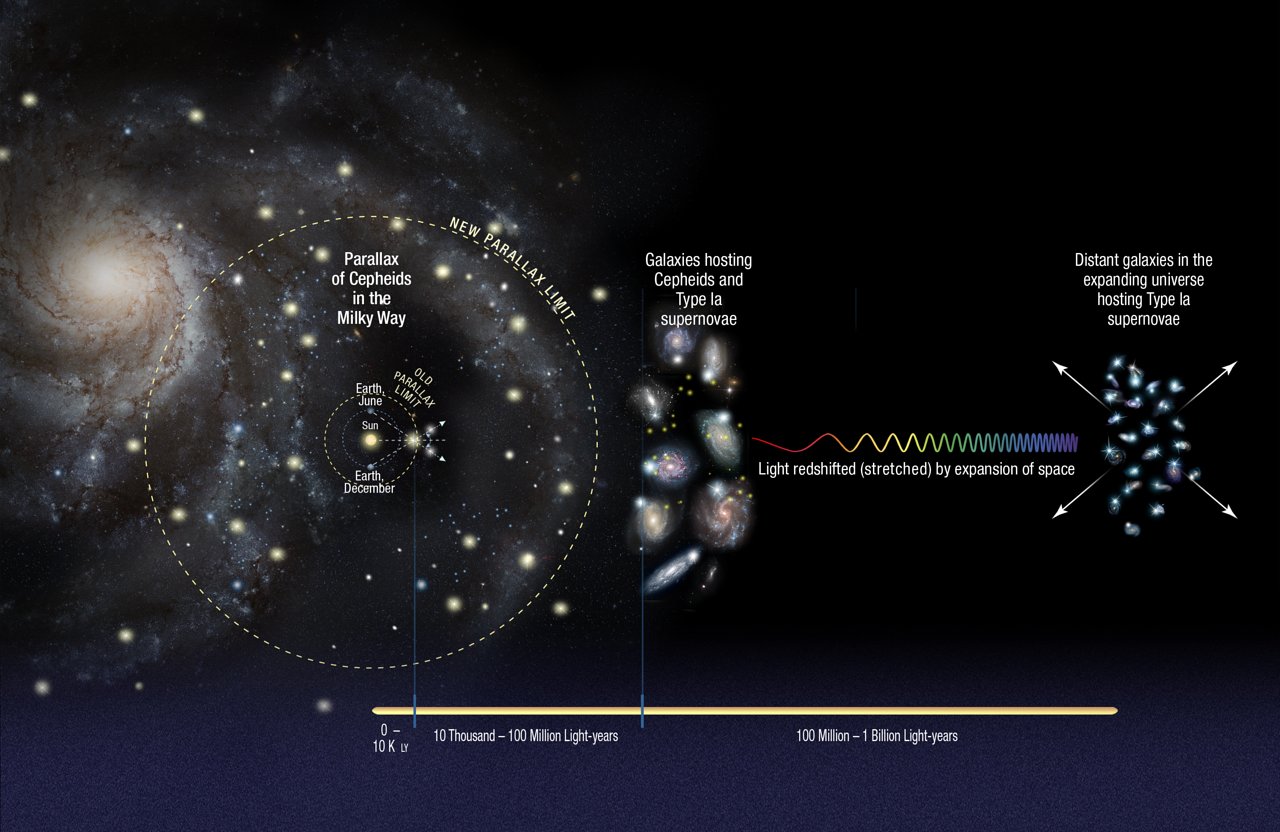 Parallax measurements may be an important clue to understanding three of the universe's most elusive components: dark matter, dark energy and neutrinos.[12] 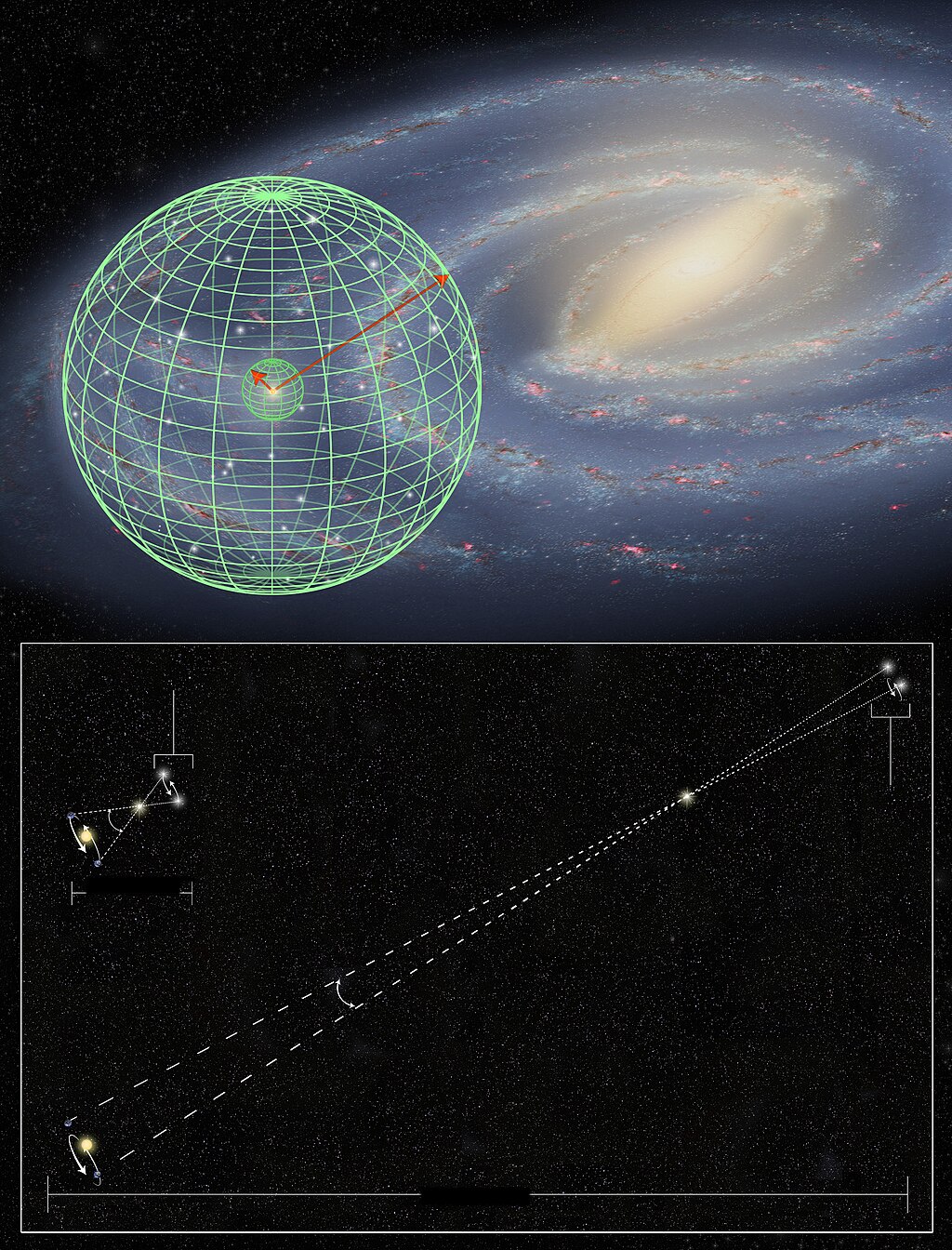 Hubble Space Telescope precision stellar distance measurement has been extended 10 times further into the Milky Way.[13] The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, while for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of observed stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the uncertainty is inversely proportional to the square root of the sample size.[14] Moving cluster parallax is a technique where the motions of individual stars in a nearby star cluster can be used to find the distance to the cluster. Only open clusters are near enough for this technique to be useful. In particular the distance obtained for the Hyades has historically been an important step in the distance ladder. Other individual objects can have fundamental distance estimates made for them under special circumstances. If the expansion of a gas cloud, like a supernova remnant or planetary nebula, can be observed over time, then an expansion parallax distance to that cloud can be estimated. Those measurements however suffer from uncertainties in the deviation of the object from sphericity. Binary stars which are both visual and spectroscopic binaries also can have their distance estimated by similar means, and do not suffer from the above geometric uncertainty. The common characteristic to these methods is that a measurement of angular motion is combined with a measurement of the absolute velocity (usually obtained via the Doppler effect). The distance estimate comes from computing how far the object must be to make its observed absolute velocity appear with the observed angular motion. Expansion parallaxes in particular can give fundamental distance estimates for objects that are very far, because supernova ejecta have large expansion velocities and large sizes (compared to stars). Further, they can be observed with radio interferometers which can measure very small angular motions. These combine to provide fundamental distance estimates to supernovae in other galaxies.[15] Though valuable, such cases are quite rare, so they serve as important consistency checks on the distance ladder rather than workhorse steps by themselves. |
天文学 このセクションは、天文学における視差からの抜粋である。[編集]  恒星視差の動き。頂角の半分が視差角である。  視差とは、ある点から引かれる線のなす角である。上図では、軌道上の地球が太陽から引かれる視差角を掃く。下図では、地動説モデルにおいて太陽が掃く視差 角が等しいことを示している。恒星についても同様の図が描けるが、視差の角度はごくわずかである。 天文学における最も重要な基本的な距離測定は、恒星視差法で用いられる三角視差によるものである。地球が太陽の周りを公転する際に、背景のより遠い星に対 して近くの星の位置がわずかに移動して見える。この移動は二等辺三角形の角度であり、2AU(地球の公転軌道の最遠点間の距離)が三角形の底辺となり、星 までの距離が等しい長さの2辺となる。最も近い恒星でも、1パーセク(3.26光年)離れた天体は1秒角のずれとなり、それ以降は距離が遠くなるにつれて 角度が減少する。天文学者は通常、距離をパーセク(視差秒角)単位で表す。一般メディアでは光年が使用される。 恒星までの距離が大きくなるほど視差は小さくなるため、測定精度の数倍以上の視差が得られるほど近い恒星でなければ、有効な距離を測定することはできな い。例えば、1990年代に実施されたヒッパルコス計画では、10万を超える恒星の視差を約1ミリ秒角の精度で測定し、数百パーセクまでの恒星の有効な距 離を測定した。ハッブル宇宙望遠鏡の広視野カメラ3は、20~40マイクロ秒角の精度で測定できる可能性があり、少数の星については5,000パーセク (16,000光年)までの信頼性の高い距離測定が可能である。[8][9] ガイア宇宙ミッションは、15等級より明るいほとんどの星について同様に正確な距離を提供した。[10] 距離は、約3万光年離れた銀河中心まで10%以内の精度で測定できる。恒星は太陽に対して相対速度を持っており、それによって視差(空を横切る動き)と視 線速度(太陽に向かうまたは太陽から遠ざかる動き)が生じる。前者は恒星の位置の変化を長年にわたってプロットすることで決定され、後者は視線に沿った動 きによって生じる恒星スペクトルのドップラー効果を測定することで得られる。同じスペクトル分類で、ほぼ同等の等級の範囲にある恒星のグループについて は、視線速度に対する固有運動の統計的分析から平均視差を導くことができる。この統計的視差法は、50パーセクを超える明るい恒星やケフェウス座やりゅう こつ座などの巨大変光星の距離測定に有効である。  視差測定は、宇宙で最も捉えどころのない3つの要素、すなわち暗黒物質、暗黒エネルギー、ニュートリノを理解する重要な手がかりとなる可能性がある。  ハッブル宇宙望遠鏡による恒星の精密距離測定は、銀河系内で10倍に拡大された。 太陽の空間運動は、視差測定の精度を高めるより長い基線を提供し、これを「年周視差」と呼ぶ。天の川円盤内の恒星については、これは1年あたり平均4AU のベースラインに相当し、一方、ハロー星については1年あたり40AUのベースラインとなる。数十年後には、ベースラインは従来の視差測定で使用されてい た地球-太陽間のベースラインよりも桁違いに大きくなる可能性がある。しかし、恒星の相対速度が未知数であるため、視差測定にはより高いレベルの不確実性 が伴う。複数の星のサンプルに適用すると、不確実性は低減できる。不確実性はサンプルサイズの平方根に反比例する。 移動星団視差は、近傍の星団における個々の星の動きを利用して、その星団までの距離を求める手法である。この手法が有効なほど近傍にあるのは散開星団のみ である。特にヒアデス星団の距離は、歴史的に距離測定の重要なステップとなってきた。 その他の個々の天体についても、特別な状況下では基本的な距離推定を行うことができる。超新星残骸や惑星状星雲のようなガス雲の膨張が長期間にわたって観 測できる場合、その雲までの膨張視差距離を推定することができる。しかし、これらの測定値は、天体の球体からの逸脱の不確実性に影響を受ける。また、視覚 的および分光測光的に二重星である天体も、同様の方法で距離を推定することができ、上記の幾何学的不確実性の影響を受けない。これらの方法に共通する特徴 は、角運動量の測定値が絶対速度(通常はドップラー効果によって得られる)の測定値と組み合わされていることである。距離の推定値は、観測された絶対速度 が観測された角運動量に見えるように、対象物がどの程度離れていなければならないかを計算することによって得られる。 特に膨張視差は、超新星の放出物が大きな膨張速度と大きなサイズ(恒星と比較して)を持つため、非常に遠い対象物の基本的な距離推定値を与えることができ る。さらに、超新星は非常に小さな角運動を測定できる電波干渉計で観測できる。これらの組み合わせにより、他の銀河にある超新星の距離を基本的な方法で推 定できる。[15] このようなケースは貴重ではあるが、非常にまれであるため、それ自体が主要なステップとなることはなく、距離の階層における重要な整合性チェックとして機 能する。 |
Metrology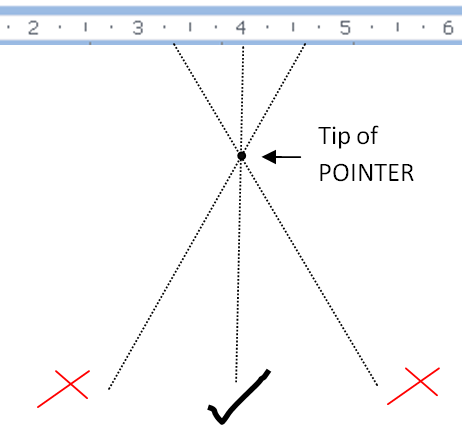 The correct line of sight needs to be used to avoid parallax error. Measurements made by viewing the position of some marker relative to something to be measured are subject to parallax error if the marker is some distance away from the object of measurement and not viewed from the correct position. For example, if measuring the distance between two ticks on a line with a ruler marked on its top surface, the thickness of the ruler will separate its markings from the ticks. If viewed from a position not exactly perpendicular to the ruler, the apparent position will shift and the reading will be less accurate than the ruler is capable of. A similar error occurs when reading the position of a pointer against a scale in an instrument such as an analog multimeter. To help the user avoid this problem, the scale is sometimes printed above a narrow strip of mirror, and the user's eye is positioned so that the pointer obscures its reflection, guaranteeing that the user's line of sight is perpendicular to the mirror and therefore to the scale. The same effect alters the speed read on a car's speedometer by a driver in front of it and a passenger off to the side, values read from a graticule, not in actual contact with the display on an oscilloscope, etc. |
計測 視差エラーを避けるには、正しい視線を使用する必要がある。 測定対象物に対するマーカーの位置を視認して測定を行う場合、マーカーが測定対象物からある程度離れており、正しい位置から視認されていないと、視差エ ラーが発生する可能性がある。例えば、上面に目盛りが刻まれた定規を使用して、線上の2つの目盛り間の距離を測定する場合、定規の厚みによって目盛りと目 盛りの間隔が離れてしまう。定規に対して正確に垂直でない位置から見た場合、見かけ上の位置がずれてしまい、定規の読み取り精度よりも正確性が低下する。 アナログ式のマルチメーターのような機器で目盛りを読み取る際にも、同様の誤差が生じる。この問題を回避するために、目盛りは狭いミラー帯の上に印刷され ることがあり、ユーザーの視線が目盛りの反射を隠すように位置が決められる。これにより、ユーザーの視線はミラーに対して、そしてしたがって目盛りに対し ても垂直になることが保証される。同じ効果が、前方を走る車のスピードメーターの速度表示を、前方を走る車の運転手と横に並走する同乗者で異なるものに見 せる。また、オシロスコープのディスプレイに実際に触れることなく、グリッドから読み取った値などにも同じことが言える。 |
| Photogrammetry Main article: Photogrammetry When viewed through a stereo viewer, aerial picture pair offers a pronounced stereo effect of landscape and buildings. High buildings appear to "keel over" in the direction away from the center of the photograph. Measurements of this parallax are used to deduce the height of the buildings, provided that flying height and baseline distances are known. This is a key component of the process of photogrammetry. |
写真測量 詳細は「写真測量」を参照 ステレオビューアーで見る場合、航空写真のペアは、風景や建物について顕著な立体視効果を提供する。高い建物は、写真の中心から離れる方向に「傾いて」見 える。飛行高度とベースライン距離が分かっている場合、この視差の測定値は建物の高さを推定するために使用される。これは写真測量のプロセスの重要な要素 である。 |
| Photography Parallax error can be seen when taking photos with many types of cameras, such as twin-lens reflex cameras and those including viewfinders (such as rangefinder cameras). In such cameras, the eye sees the subject through different optics (the viewfinder, or a second lens) than the one through which the photo is taken. As the viewfinder is often found above the lens of the camera, photos with parallax error are often slightly lower than intended, the classic example being the image of a person with their head cropped off. This problem is addressed in single-lens reflex cameras, in which the viewfinder sees through the same lens through which the photo is taken (with the aid of a movable mirror), thus avoiding parallax error. Parallax is also an issue in image stitching, such as for panoramas. Contax III rangefinder camera with macro photography setting. Because the viewfinder is on top of the lens and near the subject, goggles are fitted in front of the rangefinder and a dedicated viewfinder is installed to compensate for parallax.  Failed panoramic image due to the parallax, since the axis of rotation of the tripod is not the same as the focal point. |
写真 視差エラーは、二眼レフカメラやレンジファインダーカメラなど、多くの種類のカメラで写真を撮影する際に発生する。このようなカメラでは、被写体を見るた めの光学機器(ビューファインダーまたは2つ目のレンズ)と、写真を撮影するための光学機器が異なる。ファインダーはカメラのレンズの上部に位置している ことが多いため、視差エラーのある写真は意図したよりもやや下にずれてしまい、典型的な例としては人物の頭が切り取られたような画像になる。この問題は一 眼レフカメラでは対処されており、ファインダーは写真撮影用のレンズと同じレンズを通して見えるようになっており(可動ミラーの助けを借りて)、視差エ ラーを回避している。 視差は、パノラマ写真のような画像のつなぎ合わせでも問題となる。 マクロ撮影設定のコンタックスIII型レンジファインダーカメラ。ファインダーがレンズの上部で被写体に近いため、レンジファインダーの前にゴーグルが取 り付けられ、視差を補正するための専用ファインダーが設置されている。  三脚の回転軸と焦点が一致していないため、視差によりパノラマ画像が失敗している。 |
| Weapon sights Parallax affects sighting devices of ranged weapons in many ways. On sights fitted on small arms and bows, etc., the perpendicular distance between the sight and the weapon's launch axis (e.g. the bore axis of a gun)—generally referred to as "sight height"—can induce significant aiming errors when shooting at close range, particularly when shooting at small targets.[16] This parallax error is compensated for (when needed) via calculations that also take in other variables such as bullet drop, windage, and the distance at which the target is expected to be.[17] Sight height can be used to advantage when "sighting in" rifles for field use. A typical hunting rifle (.222 with telescopic sights) sighted in at 75m will still be useful from 50 to 200 m (55 to 219 yd) without needing further adjustment.[citation needed] Optical sights Further information: Telescopic sight § Parallax compensation 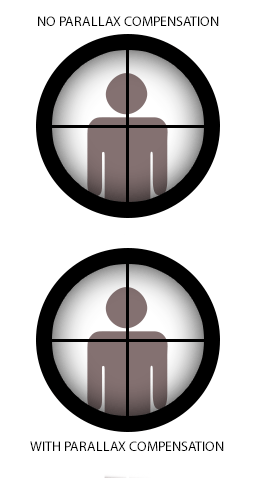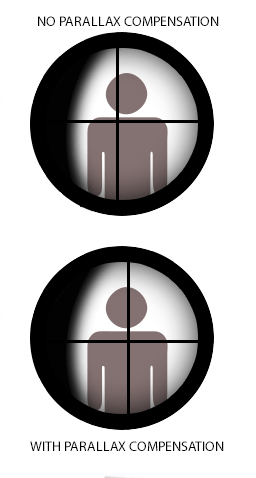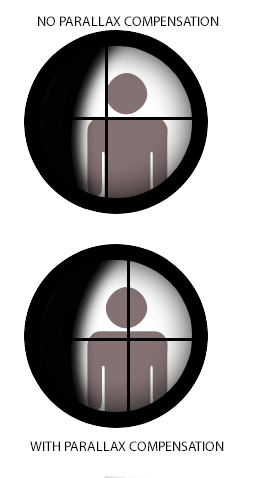 Simple animation demonstrating the effects of parallax compensation in telescopic sights, as the eye moves relative to the sight. In some reticled optical instruments such as telescopes, microscopes or in telescopic sights ("scopes") used on small arms and theodolites, parallax can create problems when the reticle is not coincident with the focal plane of the target image. This is because when the reticle and the target are not at the same focus, the optically corresponded distances being projected through the eyepiece are also different, and the user's eye will register the difference in parallaxes between the reticle and the target (whenever eye position changes) as a relative displacement on top of each other. The term parallax shift refers to the resultant apparent "floating" movements of the reticle over the target image when the user moves his/her head/eye laterally (up/down or left/right) behind the sight,[18] i.e. an error where the reticle does not stay aligned with the user's optical axis. Some firearm scopes are equipped with a parallax compensation mechanism, which consists of a movable optical element that enables the optical system to shift the focus of the target image at varying distances into the same optical plane of the reticle (or vice versa). Many low-tier telescopic sights may have no parallax compensation because in practice they can still perform very acceptably without eliminating parallax shift. In this case, the scope is often set fixed at a designated parallax-free distance that best suits their intended usage. Typical standard factory parallax-free distances for hunting scopes are 100 yd (or 90 m) to make them suited for hunting shots that rarely exceed 300 yd/m. Some competition and military-style scopes without parallax compensation may be adjusted to be parallax free at ranges up to 300 yd/m to make them better suited for aiming at longer ranges. [citation needed] Scopes for guns with shorter practical ranges, such as airguns, rimfire rifles, shotguns, and muzzleloaders, will have parallax settings for shorter distances, commonly 50 m (55 yd) for rimfire scopes and 100 m (110 yd) for shotguns and muzzleloaders. [citation needed] Airgun scopes are very often found with adjustable parallax, usually in the form of an adjustable objective (or "AO" for short) design, and may adjust down to as near as 3 metres (3.3 yd).[citation needed] Non-magnifying reflector or "reflex" sights can be theoretically "parallax free". But since these sights use parallel collimated light this is only true when the target is at infinity. At finite distances, eye movement perpendicular to the device will cause parallax movement in the reticle image in exact relationship to the eye position in the cylindrical column of light created by the collimating optics.[19][20] Firearm sights, such as some red dot sights, try to correct for this via not focusing the reticle at infinity, but instead at some finite distance, a designed target range where the reticle will show very little movement due to parallax.[19] Some manufacturers market reflector sight models they call "parallax free",[21] but this refers to an optical system that compensates for off axis spherical aberration, an optical error induced by the spherical mirror used in the sight that can cause the reticle position to diverge off the sight's optical axis with change in eye position.[22][23] |
照準器 視差は、さまざまな方法で遠距離武器の照準装置に影響を与える。小銃や弓などに装着された照準器では、照準器と銃身軸(銃の銃身の軸)などの武器の発射軸 との垂直距離(一般的に「照準高さ」と呼ばれる)が、近距離での射撃、特に小さな標的を狙った射撃の場合に、重大な照準エラーを引き起こす可能性がある。 6] この視差による誤差は、弾丸の落下、風による影響、標的までの距離などの他の変数も考慮した計算によって(必要に応じて)補正される。[17] ライフル銃を野外で使用するために「照準を合わせる」際には、照星高が有利に働く。一般的なハンティング用ライフル(.222口径で望遠照準器付き)は、 75mで照準を合わせた場合、50mから200m(55ヤードから219ヤード)の範囲では、それ以上の調整を必要とせずに使用できる。 光学照準器 詳細情報: 望遠照準器 § 視差補正  照準器に対して目が動く場合の、望遠照準器における視差補正の効果を示す簡単なアニメーション。 望遠鏡、顕微鏡、あるいは小銃やセオドライトで使用される望遠照準器(「スコープ」)などのレチクル光学機器では、レチクルがターゲット像の焦点面と一致 していない場合、視差が問題を引き起こす可能性がある。これは、レチクルとターゲットが同じ焦点にない場合、接眼レンズを通して投影される光学的に対応す る距離も異なり、ユーザーの目には、レチクルとターゲットの間の視差の差異が(目の位置が変わるたびに)互いに重なり合った相対的な変位として認識される ためである。視差シフトという用語は、ユーザーが照準器の後ろで頭や目を左右(上下または左右)に動かしたときに、標的像の上でレチクルが「浮遊」してい るように見える結果的な動きを指す。すなわち、レチクルがユーザーの光軸と一直線上に並ばないエラーである。 一部の銃用スコープには視差補正機構が装備されており、可動式光学素子により、光学システムがターゲット画像の焦点を、レティクルの同一光学平面(または その逆)に、距離に応じてシフトさせることができる。多くの低価格の望遠照準器では、視差補正が不要な場合がある。なぜなら、実際には視差シフトを排除し なくても、非常に優れたパフォーマンスを発揮できるからだ。この場合、スコープは、使用目的に最適な指定のパララックスフリー距離に固定されることが多 い。ハンティングスコープの一般的な標準的なパララックスフリー距離は、100ヤード(または90メートル)であり、300ヤード/メートルを超えること はほとんどないハンティングショットに適している。視差補正機能のない競技用や軍用スコープの中には、より遠距離を狙いやすくするために、300ヤード/ メートルまでの範囲で視差をなくすよう調整されているものもある。[要出典] 空気銃、リムファイア・ライフル、散弾銃、銃口装填銃など、実用的な射程距離が短い銃用のスコープでは、より短い距離用の視差設定があり、一般的にリム ファイア・スコープでは50m(55yd)、散弾銃と銃口装填銃では100m(110yd)である。[要出典] 空気銃用スコープは、可変パララックス機能を備えていることが非常に多く、通常は可変対物レンズ(または略して「AO」)設計の形式で、3メートル (3.3ヤード)に近い距離まで調整できる場合がある。[要出典] 反射式照準器や「レフレックス」照準器は、理論的には「パララックスフリー」である。しかし、これらの照準器は平行な平行光線を使用しているため、これは ターゲットが無限遠にある場合のみ当てはまる。有限の距離では、照準器に対して垂直な目の動きは、平行光学系によって生み出される円柱状の光の柱における 目の位置と正確に一致する視差運動をレチクル像に引き起こす。[19][20] 銃器の照準器、例えば一部のレッドドットサイトは、レチクルを無限遠に焦点を合わせるのではなく、代わりにある有限の距離、すなわちレチクルが視差による 動きをほとんど示さないように設計された照準距離に焦点を合わせることで、これを補正しようとしている。。一部のメーカーは「パララックスフリー」と称す る反射式照準器モデルを販売しているが[21]、これは軸外球面収差を補正する光学システムを指しており、これは照準器で使用される球面鏡によって引き起 こされる光学エラーであり、目の位置が変わると照準器の光軸からレチクルの位置が外れる原因となる。[22][23] |
| Artillery-fire Because of the positioning of field or naval artillery, each gun has a slightly different perspective of the target relative to the location of the fire-control system. When aiming guns at the target, the fire control system must compensate for parallax to assure that fire from each gun converges on the target. |
砲撃 野砲や艦砲の位置により、射撃統制装置の場所と相対的に、各砲から見た目標の視点は微妙に異なる。砲を標的に向ける際、射撃統制システムは視差を補正し、 各砲から発射される砲弾が標的に収束するようにしなければならない。 |
| Art Several of Mark Renn's sculptural works play with parallax, appearing abstract until viewed from a specific angle. One such sculpture is The Darwin Gate (pictured) in Shrewsbury, England, which from a certain angle appears to form a dome, according to Historic England, in "the form of a Saxon helmet with a Norman window... inspired by features of St Mary's Church which was attended by Charles Darwin as a boy".[24]  their separate columns, each arched at the top an apparent dome Viewed from a certain angle the curves of the three separate columns of The Darwin Gate appear to form a dome |
アート マーク・レンの彫刻作品のいくつかは視差を利用しており、特定の角度から見ないと抽象的な作品に見える。 イングランドのシュルーズベリーにある「ダーウィン・ゲート」(写真)もその一つで、特定の角度から見るとドームのように見える。 イングランド歴史協会によると、「ノルマン様式の窓を備えたサクソン人の兜の形をしており、少年時代にチャールズ・ダーウィンが通っていたセント・メア リー教会の特徴から着想を得ている」という。[24]  それぞれ独立した円柱は、上部がアーチ状になっており、 それぞれ独立した円柱は、上部がアーチ状になっており、ドームのように見える ある角度から見ると、3本の独立した円柱からなる「ダーウィン・ゲート」の曲線がドームのように見える |
| As a metaphor In a philosophic/geometric sense: an apparent change in the direction of an object, caused by a change in observational position that provides a new line of sight. The apparent displacement, or difference of position, of an object, as seen from two different stations, or points of view. In contemporary writing, parallax can also be the same story, or a similar story from approximately the same timeline, from one book, told from a different perspective in another book. The word and concept feature prominently in James Joyce's 1922 novel, Ulysses. Orson Scott Card also used the term when referring to Ender's Shadow as compared to Ender's Game. The metaphor is invoked by Slovenian philosopher Slavoj Žižek in his 2006 book The Parallax View, borrowing the concept of "parallax view" from the Japanese philosopher and literary critic Kojin Karatani. Žižek notes The philosophical twist to be added (to parallax), of course, is that the observed distance is not simply "subjective", since the same object that exists "out there" is seen from two different stances or points of view. It is rather that, as Hegel would have put it, subject and object are inherently "mediated" so that an "epistemological" shift in the subject's point of view always reflects an "ontological" shift in the object itself. Or—to put it in Lacanese—the subject's gaze is always already inscribed into the perceived object itself, in the guise of its "blind spot," that which is "in the object more than the object itself," the point from which the object itself returns the gaze. "Sure the picture is in my eye, but I am also in the picture"...[25] — Slavoj Žižek, The Parallax View https://en.wikipedia.org/wiki/Parallax |
比喩として 哲学的・幾何学的な意味において:観察位置の変化によって生じる、物体の方向の見かけ上の変化。2つの異なる場所や視点から見た場合の見かけ上の位置のず れ、または位置の違い。現代の文章では、視差は同じ話、またはほぼ同じ時間軸の類似した話であり、ある本から別の視点で語られた別の本のことである。この 言葉と概念は、ジェイムズ・ジョイスの1922年の小説『ユリシーズ』でも顕著に用いられている。また、オーソン・スコット・カードは『エンダーの影』を 『エンダーのゲーム』と比較した際に、この用語を使用している。 この比喩は、スロベニアの哲学者スラヴォイ・ジジェクが2006年に出版した著書『パララックス・ビュー』で用いられている。この「パララックス・ ビュー」という概念は、日本の哲学者で文芸評論家の柄谷行人から借用したものである。ジジェクは次のように指摘している。 (視差に)加えられる哲学的ひねりとは、もちろん、観察される距離は単純に「主観的」なものではないということだ。なぜなら、「そこ」に存在する同じ対象 が、2つの異なる立場や視点から見られるからだ。むしろ、ヘーゲルが言うように、主体と対象は本質的に「媒介」されているため、主体の視点における「認識 論的」な変化は、常に対象自体における「存在論的」な変化を反映している。あるいは、ラカネ派の言葉で言えば、主観の視線は常にすでに知覚された対象その ものに刻み込まれている。それは「盲点」という形で、「対象そのものよりも対象の中にある」ものであり、そこから対象そのものが視線を返す。「確かに絵は 私の目の中にあるが、私もまた絵の中にある」...[25] —スラヴォイ・ジジェク、『パララックス・ビュー』 https://en.wikipedia.org/wiki/Parallax |
| Binocular disparity Lutz–Kelker bias Parallax mapping, in computer graphics Parallax scrolling, in computer graphics Spectroscopic parallax Triangulation, wherein a point is calculated given its angles from other known points Trigonometry True range multilateration, wherein a point is calculated given its distances from other known points Xallarap |
両眼視差 ルッツ・ケルカーのバイアス コンピュータグラフィックスにおける視差マッピング コンピュータグラフィックスにおける視差スクロール 分光視差 三角測量、既知の点からの角度から点を計算する 三角法 真の距離多辺測量、既知の点からの距離から点を計算する Xallarap |
| https://en.wikipedia.org/wiki/Parallax |
|
★オ リジナルの写真(左: 但し左右反転)と画像修正後(右)の写真——こうなると何が「オリジナル」で何が「修正」で何が「フェイク」なのかわかりにくくなりますね。真実 性の崩壊っていうのでしょうか?でももともと「写真」という名前が真実を写したものということなので「真実」の反映であり、それ(=写真そのももの)はオ リジナルじゃないとも言えますね。これが、パララックス(視差; Parallax)の意味でしょう。——柄谷 行人やスラヴォイ・ジジェクのいう(→「有馬稲子のパラ ラックス」)。


リ ンク
文 献
そ の他の情報
Copyleft, CC, Mitzub'ixi Quq Chi'j, 1996-2099
☆
 ☆
☆