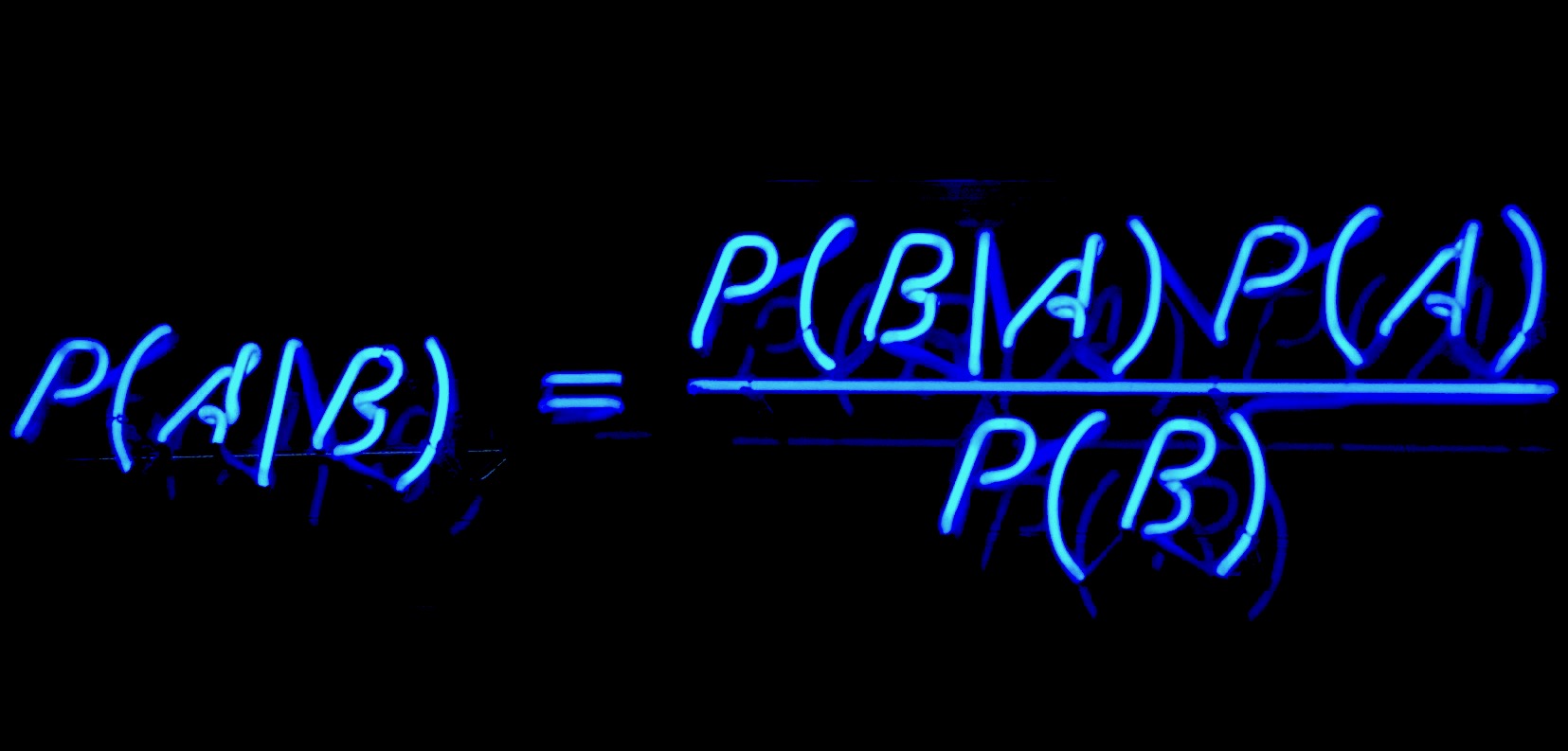▼プリントアウトにかんする許 諾情報▲ 種の連続性/非連続性 と進化に関する方法論 ▼ はじめての方は*こ こをクリック* ▼

池田光穂
最大節約法 Maximum parsimony
「入力データはある範囲のタクソ
ンの形質である。形質としてはある性質の有無という二分法の値(たとえば尾の有無)、あるいはゲノムの特定部位におけるDNA塩基や、タンパク質のアミノ
酸残基も用いられる……最大節約法で用いられる系統樹は一般に無根系統樹(時間経過を考慮せずタクソン間の関係だけを示す系統樹)である。この方法で用い
られるすべてのタクソンは木の中の葉に当たる末端のノードである(従ってそれに至るエッジは各1本しかない)。木の内部のノードは推定される祖先種であ
る。各内部ノードには3本のエッジがある。各形質間の変化はいずれかのエッジに相当する。最大節約法は、考えられるすべての系統樹の中から、形質の変化の
数が最も少ない(または他のものと等しくてもよい)ものを選択する方法である。このために、すべての系統樹について、それを説明できる最小限の変化の数を
「長さ」として与え、この長さが一番小さいのが最大節約系統樹」(出典:ウィ
キ日語)
近隣結合法 neighbor-joining method, NJ
「系統樹を作製するためのボトム
アップ式のクラスタ解析法である。日本の斎藤成也・根井正利が分子系統樹を作成する方法として1987年に発表……。普通DNAの塩基配列やタンパク質の
一次構造に基づいて系統樹を作製するのに用いられる方法で、計算には各タクソン(生物種あるいは配列)のペア間の距離を知ることが必要。……近隣結合法は
系統樹の最小進化基準、つまりアルゴリズムの各段階で全ての枝の長さの合計が最小となるようなトポロジーが望ましいという基準に基づいている。しかし系統
樹を段階的に構成するアルゴリズムであるため、最終的に全枝長を最小にする本当のトポロジーが明らかになるとは限らない。この意味では最適な方法とまでは
いえないが、すでに詳細に検討されており、最適なものに非常に近い系統樹が得られる。近隣結合法の最大の利点は効率であって、ほかの系統解析法(最大節約
法、最尤法、ベイズ法など)では計算能力的に不可能なほどの大量のデータセットも扱うことが可能」(出典:ウィキ日語)
最尤法(さいゆうほう), Maximum likelihood estimation, MLE
「与えられたデータからそれが従 う確率分布の母数について推測するためによく用いられる方法で、尤度の概念を利用するものである。この方法はロナルド・フィッシャーが1912年から 1922年にかけて開発……。」(出典:ウィキ日語)
非加重結合法, Unweighted Pair Group Method with Arithmetic mean, UPGMA
「系統樹を作製するためのボトム アップ式のクラスタ解析法である。入力データは対象の各ペア間の距離であり、有根系統樹が作製される。進化速度が一定(分子時計仮説)と仮定して有根系統 樹を作製するのにときどき用いられる。最初に、各対象がそれぞれ1つのクラスタを作っているとする。その後段階的に最も近いクラスタを結合して上位のクラ スタとする。2つのクラスタAとBについて、AとBそれぞれの要素すべての間の距離の平均をとって、これをAとBの間の距離とする。」(出典:ウィキ日語)
ベイズ法(ベイズ推定), Bayesian inference
「ベイズ確率の考え方に基づき、 観測事象(観測された事実)から、推定したい事柄(それの起因である原因事象)を、確率的な意味で推論すること」(出典:ウィキ日語)
【ベイズ確率】「ベイズ主義による「確率」の考え方(およびその値)を
指す。すなわち複数の命題(¥,¥theta_1,¥theta_2,¥ldots)の各々の尤もらしさ(あるいはその根拠となる信念・信頼の度合)を確
率値(¥,p_1,p_2,¥ldots)と見なす。主観確率理論の一つ」ベイズ主義による「確率」の考え方(およびその値)を指す。すなわち複数の命題
(¥,¥theta_1,¥theta_2,¥ldots)の各々の尤もらしさ(あるいはその根拠となる信念・信頼の度合)を確率値(¥,p_1,
p_2,¥ldots)と見なす。主観確率理論の一つ
系統学
「生物の種の系統的な発生、つま り生物の進化による系統分化の歴史を研究する学問。種や系統群の分化と進化を研究目的とする」(出典:ウィキ日語)
系統樹
「生物の進化やその分かれた道筋 を枝分かれした図として示したものである。樹木の枝分かれのように描かれる」(出典:ウィキ日語)
分子系統学
「生物のもつタンパク質のアミノ 酸配列や遺伝子の塩基配列を用いて系統解析を行い、生物が進化してきた道筋(系統)を理解しようとする学問」(出典:ウィキ日語)
哲学 と連続性の概念について
「あらゆる概念のなかで、連続性の概 念ほど哲学が取り扱いに困難を覚える概念はない」——チャールズ・サンダー・パース『連続性の哲学』伊藤邦武編訳,p.223、岩波文庫

Copyright Mitzub'ixi Quq Chi'j, 2099