推論を、前提条件、結論、規則という観点 から規定すると、

• 前提条件（precondition）：A

• 結論（conclusion）：B

• 規則（rule）：「前提条件は規則を含意すること」により、Ａ→Ｂ
  

A：雨が降るという現象

B：土が湿っている現象

さて、Ａ→Ｂ を説明する方法には、少なくとも次の３つの方法がある。すなわち、（i） 演繹（deduction）、（ii）帰納（induction）、（iii）仮説推論＝アブダクション （abduction）である。

（i）演繹 （deduction）：Ａの帰結としてＢを導くことを可能にする。「雨がふると、土が湿る。雨が降っている。その土は 湿ってる」A：雨と いう現象、Ｂ：土が湿っている状態

（ii）帰納 （induction）：ＡがＢを必然的にともなうとき、Ｂのいくつかの事例からＡを推論することを可能にする。「これ まで、雨がふると、 土が湿ってきた。雨が降ると土は湿る」

（iii）仮説推論＝アブダク ション（abduction）：Ｂについての説明としてＡを推論することを可能にする。「土が湿ってい る。雨がふると、土が 湿る。つまり雨が降ったに違いない」。

演繹は、前提条件が正しければ結論は真で あることを示す。帰納はいくつかの後件（Ｂ）を観察した結果として前件（Ａ)を蓋然的に推論する。それ に対して仮説推論（アブダクション）は、前提条件（A）が、その帰結（Ｂ）から推論されることを可能にする。つまりアブダクションは、前提条件を観察して いなくても、それが起こったことを容認する。これを、後件肯定（Affirming the consequent）という。

後件肯定は次のように命題化できる。

「もしＰならば、Qである。Qである。し たがってＰである」

これは、P=Qの場合のみ可能で、P以外 でもQを導くものがあれば、QからPを導くことには限界がある。したがって、後件肯定は、論理的には形 式的誤謬である。ラテン語では、post hoc ergo propter hoc （事後的におこったことを、前の現象がおこったことが前提となりおこったと解釈すること［の誤り］）ともいう。

したがって、仮説推論＝アブダクションは、すべて正しいことを導く論法で はなく、もっとも適切な説明を、事後的に観察された事実から推論する方 法である。

ガリレオ・ガリレイ（Galileo Galilei, 1564-1642）は、「物体の落下速度は質量と比例関係にある」という説明に対して、詳細な実験から、物体の落下速度は質 量に比例してい ないことを証明した。これは帰納に基づく証明である。このことから、質量とは無関係に落下速度は「一定」ではないかと考えた。これは仮説推論＝アブダク ションである。その後、フックやニュートンによる万有引力の法則や運動法則が定式化された。その後は、これを前提にさまざまな推論（金星での落下速度の計 算）を試みることは演繹的な方法である。

アブダクションにもとづき、かつての帰納 的な証明を、定式化し、演繹方法を定着させることができるという点で、アブダクションは、科学的推論に はなくてはならないものになっている。

【チャールズ・サンダー・パースのアブダ クション】 (CP 5.189)

• 驚くべき事実、Ｃ、が観察された。
• しかしもしＡが真実なら、Ｃは当然のこととして起こりうる。
• すなわち、Ａが真実であることを疑う理由があるのだ。

Harry G. Frankfurt, 1958. Peirce's notion of abduction. Journal of Philosophy 55 (14):593-597.

【ベイズの定理】

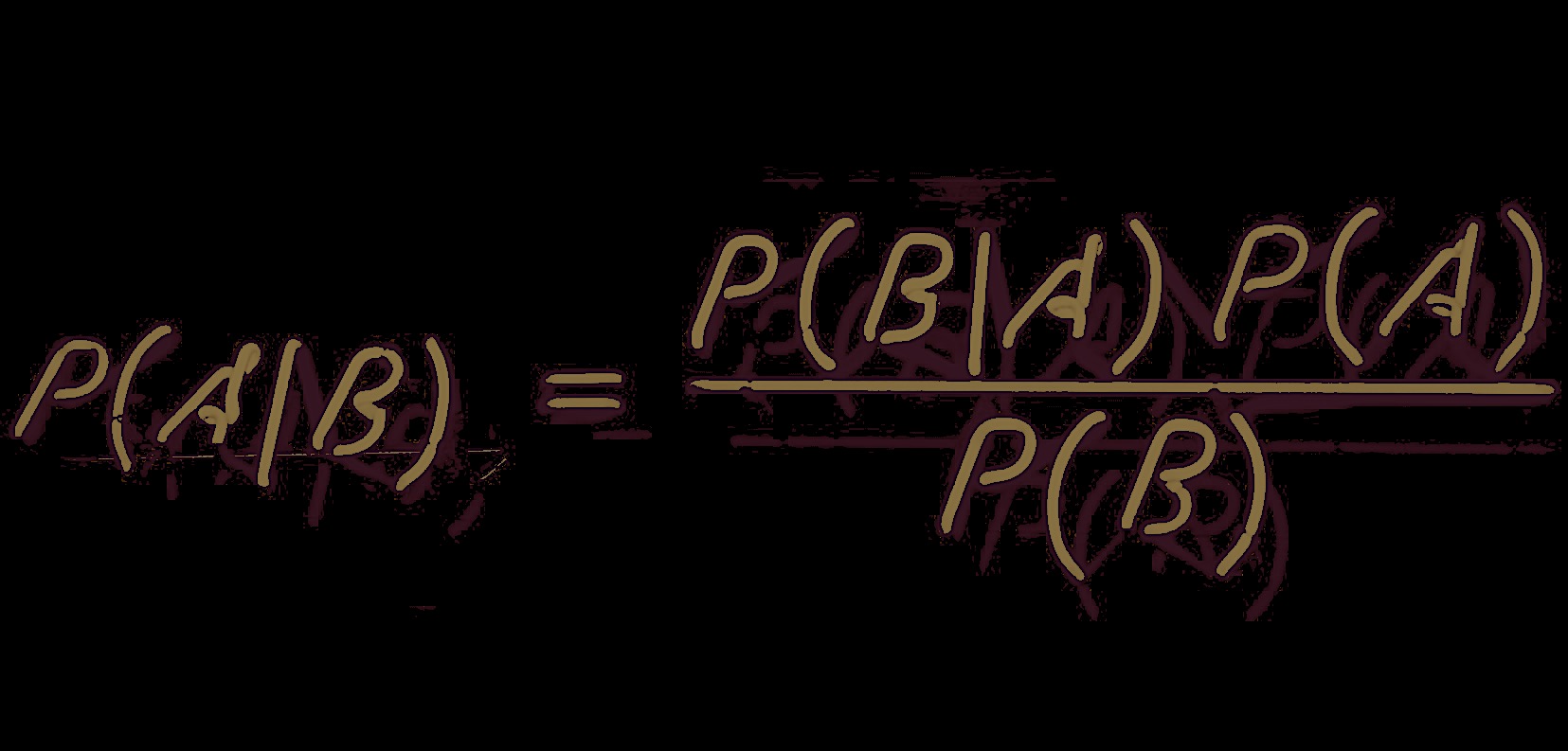
「ベイズ統計学では、事象の確率という考え方を採用し、必ずしも頻度には基づかない確率を「確率」として見なす。／またベイズの定理を用 い、事前確率及び尤度を仮定した下で事後確率を与える、という相対的なメカニズムを主張している。したがって事後確率の計算結果の信憑性や有用性は、事前分布と尤度の設定にかかっており、慎重を期すこと が必要である。これはベイズ統計学が、不確実性を含む問題を人によっ て異なる確率を用いて定式化することを許容する主観確率 (subjective probability) という立場をとっていること による。この立場はまだ解析対象となっていない新たな問題へのアプローチを可能にするという利点がある一方で、確率の決め方について客観性に欠けるという 批判もある（客観確率）」—ウィキペディア「ベイズの定理」

【余談】

アブダクションとは、ベイズ確率を確立す る個々の（均質な）手続きのような気が、私はします。ベイズ確率にくらべると、アブダクションはより緩 やかな時系列のなかでの時にアドホックな比較的長めのプロセスで、いわゆるアハ経験なども包摂されるかもしれません。アハ経験の後に、それが後件肯定とし てきちんと当人に（既存の合理的な判断材料を使って）説明できれば、それはアブダクションというのであり、ベイズの確率ような（確率分布のような）根拠を ベースに強く主張するようなものではないみたいです。

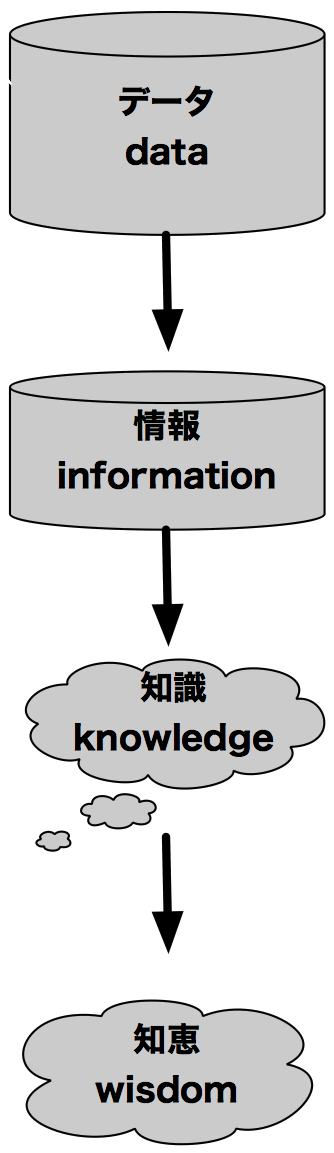図：データからの道のり（→「知の理論」より）

リンク

• Peirce on Abduction, by Stanford Encyclopedia of Philosophy
• 不品行にふるまう：行動経済学をつくる！（On Richard Thaler's Misbehaving : The Making of Behavioral Economics）
• 種の連続性／非連続性 と進化に関する方法論
  

文献

• アリストテレス『分析論前書』B25（アパゴーケー［ἀπαγωγή、apagōgē］について）
• シービオク、T.A.とJ.Y.シービオク『シャーロック・ホームズの記号論』富山太佳夫訳、岩波書店、1981年