
仮説推論
abductive
inference

推論を、前提条件、結論、規則という観点
から規定すると、
A:雨が降るという現象
B:土が湿っている現象
さて、A→B を説明する方法には、少なくとも次の3つの方法がある。すなわち、(i) 演繹(deduction)、(ii)帰納(induction)、(iii)仮説推論=アブダクション (abduction)である。
(i)演繹 (deduction):Aの帰結としてBを導くことを可能にする。「雨がふると、土が湿る。雨が降っている。その土は 湿ってる」A:雨と いう現象、B:土が湿っている状態
(ii)帰納 (induction):AがBを必然的にともなうとき、Bのいくつかの事例からAを推論することを可能にする。「これ まで、雨がふると、 土が湿ってきた。雨が降ると土は湿る」
(iii)仮説推論=アブダク ション(abduction):Bについての説明としてAを推論することを可能にする。「土が湿ってい る。雨がふると、土が 湿る。つまり雨が降ったに違いない」。
演繹は、前提条件が正しければ結論は真で あることを示す。帰納はいくつかの後件(B)を観察した結果として前件(A)を蓋然的に推論する。それ に対して仮説推論(アブダクション)は、前提条件(A)が、その帰結(B)から推論されることを可能にする。つまりアブダクションは、前提条件を観察して いなくても、それが起こったことを容認する。これを、後件肯定(Affirming the consequent)という。
後件肯定は次のように命題化できる。
「もしPならば、Qである。Qである。し たがってPである」
これは、P=Qの場合のみ可能で、P以外
でもQを導くものがあれば、QからPを導くことには限界がある。したがって、後件肯定は、論理的には形
式的誤謬である。ラテン語では、post hoc ergo propter hoc
(事後的におこったことを、前の現象がおこったことが前提となりおこったと解釈すること[の誤り])ともいう。
したがって、仮説推論=アブダクションは、すべて正しいことを導く論法で はなく、もっとも適切な説明を、事後的に観察された事実から推論する方 法である。
ガリレオ・ガリレイ(Galileo Galilei, 1564-1642)は、「物体の落下速度は質量と比例関係にある」という説明に対して、詳細な実験から、物体の落下速度は質 量に比例してい ないことを証明した。これは帰納に基づく証明である。このことから、質量とは無関係に落下速度は「一定」ではないかと考えた。これは仮説推論=アブダク ションである。その後、フックやニュートンによる万有引力の法則や運動法則が定式化された。その後は、これを前提にさまざまな推論(金星での落下速度の計 算)を試みることは演繹的な方法である。
アブダクションにもとづき、かつての帰納 的な証明を、定式化し、演繹方法を定着させることができるという点で、アブダクションは、科学的推論に はなくてはならないものになっている。
●帰納推論(inductive
reasoning)
| Inferences
are steps in reasoning, moving from premises to logical consequences;
etymologically, the word infer means to "carry forward". Inference is
theoretically traditionally divided into deduction and induction, a
distinction that in Europe dates at least to Aristotle (300s BCE).
Deduction is inference deriving logical conclusions from premises known
or assumed to be true, with the laws of valid inference being studied
in logic. Induction is inference from particular evidence to a
universal conclusion. A third type of inference is sometimes
distinguished, notably by Charles Sanders Peirce, contradistinguishing
abduction from induction. Various fields study how inference is done in practice. Human inference (i.e. how humans draw conclusions) is traditionally studied within the fields of logic, argumentation studies, and cognitive psychology; artificial intelligence researchers develop automated inference systems to emulate human inference. Statistical inference uses mathematics to draw conclusions in the presence of uncertainty. This generalizes deterministic reasoning, with the absence of uncertainty as a special case. Statistical inference uses quantitative or qualitative (categorical) data which may be subject to random variations. |
推論とは、前提から論理的帰結に至る推論のステップのことで、語源的に
はinferは「推論する」という意味である。推論は理論的には伝統的に演繹と帰納に分けられるが、この区別はヨーロッパでは少なくともアリストテレス
(紀元前300年代)にまで遡る。演繹法とは、真であることがわかっている、あるいは真であると仮定されている前提から論理的な結論を導く推論であり、論
理学では有効な推論の法則が研究されている。帰納法は、特定の証拠から普遍的な結論を導く推論である。チャールズ・サンダース・ペアースを筆頭に、第3の
タイプの推論が区別されることもある。 推論が実際にどのように行われるかは、様々な分野で研究されている。人間の推論(すなわち、人間がどのように結論を導くか)は、伝統的に論理学、論証学、 認知心理学の分野で研究されている。人工知能の研究者は、人間の推論をエミュレートする自動推論システムを開発している。統計的推論は、不確実性が存在す る中で結論を導き出すために数学を使用する。これは決定論的推論を一般化したもので、不確実性がない場合は特別なケースである。統計的推論では、ランダム な変動を受ける可能性のある量的または質的(カテゴリー)データを使用する。 |
| Definition The process by which a conclusion is inferred from multiple observations is called inductive reasoning. The conclusion may be correct or incorrect, or correct to within a certain degree of accuracy, or correct in certain situations. Conclusions inferred from multiple observations may be tested by additional observations. This definition is disputable (due to its lack of clarity. Ref: Oxford English dictionary: "induction ... 3. Logic the inference of a general law from particular instances."[clarification needed]) The definition given thus applies only when the "conclusion" is general. Two possible definitions of "inference" are: 1. A conclusion reached on the basis of evidence and reasoning. 2. The process of reaching such a conclusion. |
定義 複数の観察から結論を推論するプロセスを帰納推論という。結論は正しいか正しくないか、または一定の精度の範囲内で正しいか、特定の状況で正しいかであ る。複数の観察から推測された結論は、追加の観察によって検証されることがある。 この定義は(明確さに欠けるため)議論の余地がある。参考:オックスフォード英語辞典 「帰納法 ... 3. 特定の事例から一般的な法則を推論する論理」[clarification needed])。このように与えられた定義は、「結論」が一般的である場合にのみ適用される。 推論」の定義としては、次の2つが考えられる: 1. 証拠と推論に基づいて出される結論。 2. そのような結論に達するプロセス。 |
| https://en.wikipedia.org/wiki/Inference |
【チャールズ・サンダー・パースのアブダ クション】 (CP 5.189)
Harry G. Frankfurt, 1958. Peirce's notion of abduction. Journal
of Philosophy 55 (14):593-597.
【ベイズの定理】
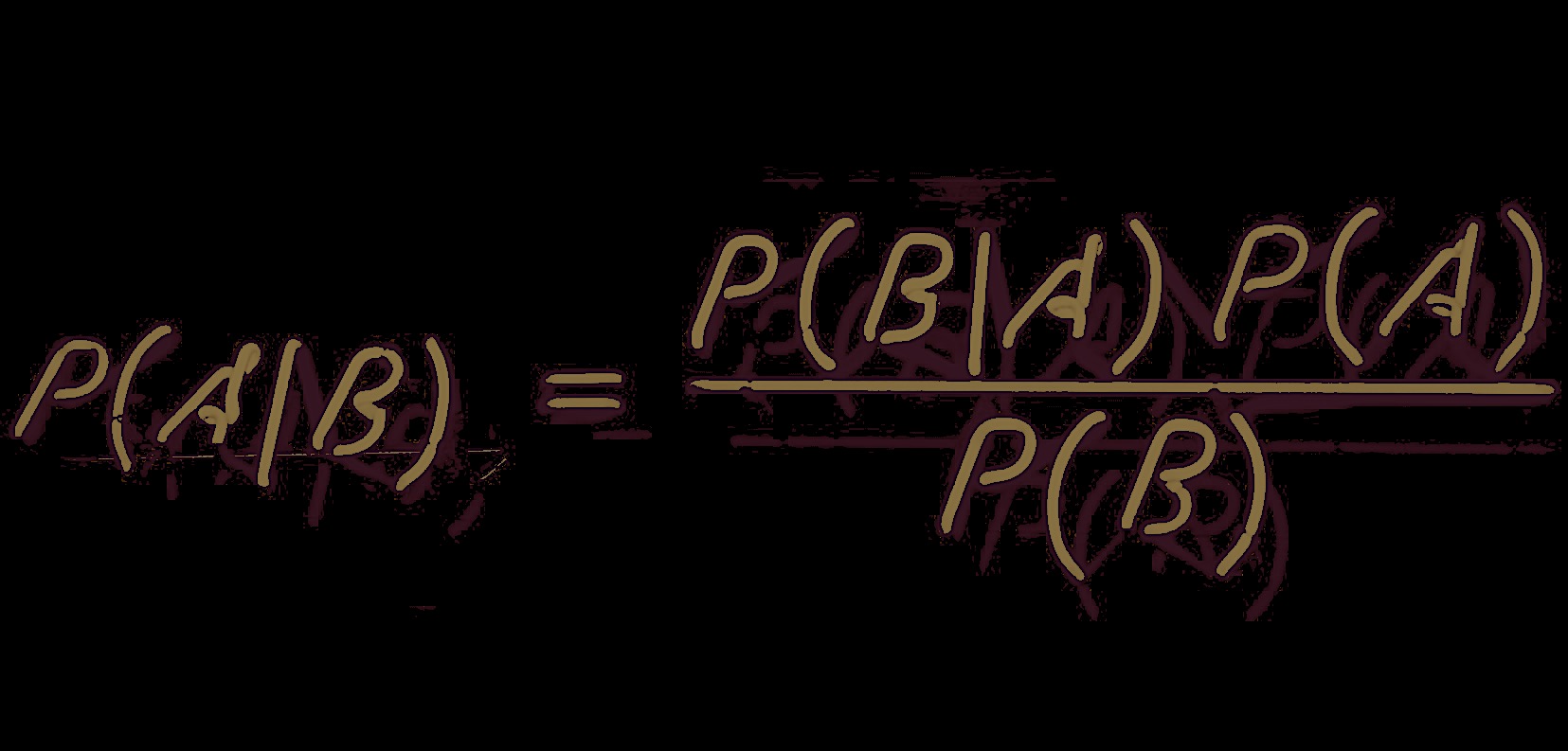
「ベイズ統計学では、事象の確率という考え方を採用し、必ずしも頻度には基づかない確率を「確率」として見なす。/またベイズの定理を用
い、事前確率及び尤度を仮定した下で事後確率を与える、という相対的なメカニズムを主張している。したがって事後確率の計算結果の信憑性や有用性は、事前分布と尤度の設定にかかっており、慎重を期すこと
が必要である。これはベイズ統計学が、不確実性を含む問題を人によっ
て異なる確率を用いて定式化することを許容する主観確率 (subjective probability) という立場をとっていること
による。この立場はまだ解析対象となっていない新たな問題へのアプローチを可能にするという利点がある一方で、確率の決め方について客観性に欠けるという
批判もある(客観確率)」—ウィキペディア「ベイズの定理」
【余談】
アブダクションとは、ベイズ確率を確立す る個々の(均質な)手続きのような気が、私はします。ベイズ確率にくらべると、アブダクションはより緩 やかな時系列のなかでの時にアドホックな比較的長めのプロセスで、いわゆるアハ経験なども包摂されるかもしれません。アハ経験の後に、それが後件肯定とし てきちんと当人に(既存の合理的な判断材料を使って)説明できれば、それはアブダクションというのであり、ベイズの確率ような(確率分布のような)根拠を ベースに強く主張するようなものではないみたいです。
 図:データからの道のり(→「知の理論」より)
図:データからの道のり(→「知の理論」より)
リンク
文献
Copyleft, CC, Mitzub'ixi Quq Chi'j, 1996-2099
Do not paste, but [Re]Think our message for all undergraduate students!!!
++
☆
 ☆
☆