ゲーム理論概説
Introduction to Game Theory

解説:池田光穂
ゲーム理論概説
Introduction to Game Theory

ゲーム理論(Game theory)の基本的解説
は、ウィキペディア(日本語、英語)を参考にしてほしい。ここでは、
ゲーム理論を学ぶための、学説史的
背景、基本用語、重要人物などを解説する。
John Von Neumann とOskar Morgenstern による『ゲームの理論と経済行動(Theory of Games and Economic Behavior)』(1944)年の公刊。
その嚆矢(および骨子)は、1928年の論文: Neumann, J. v. (1928), "Zur Theorie der Gesellschaftsspiele", Mathematische Annalen 100 (1): 295–320, doi:10.1007/BF01448847 English translation: Tucker, A. W.; Luce, R. D., eds. (1959), "On the Theory of Games of Strategy", Contributions to the Theory of Games 4, pp. 13–42
もっとも重要なポイントは、ミニマックス定理(Minimax)の主張とその証明
(1)純粋戦略と、(2)確率化された戦略 …… エミール・ボレル
純粋戦略:与えられた状況における打ち手が、毎回同 じ行為をおこなうもの。
混合戦略:与えられた状況でとりえる選択肢のなかか
らその都度異なる行為を実行するタイプの戦略。
《ミニマックス定理》――マックスの損失を最小化 (ミニマイズ)すること
すべての標準形のゼロ和2 人ゲーム(Zero-sum game) に関 する定理である。
Zero sum is a situation
in which a participant's gain or loss is exactly balanced by the losses
or gains of the other participants.
反対称的な、ペイオフ行列をもつ、ゼロ和の2人ゲー ムについて、
一方のプレイヤーにとって利得、他方のプレイヤーに 損をあらわす「唯一の数値」が存在する。各プレイヤーが、その側からみてこの数値で表せる有利な期待までは、自分の選ぶ確率化された「混合」戦略を使うこ とにより実現する。
このような戦略を「最適戦略(Optimal Strategy)」とよばれ、この唯一の数値を「ゲームのミニマックス値」と呼ぶ。
「ゲームのミニマックス値」=フォン・ノイマン=モ ルゲンシュティルンの「協力型ゲーム」の解の出発点。
「協力型ゲームでは、2つの結託へのプレイヤーのあ らゆる可能な分割が考えられ、各々の分割について対立する2つの結託の合理的な期待が、両者の間の純粋の競争的な2人だけのたたかいのミニマックス値で測 られる」(ユーラムほか 1972:205)
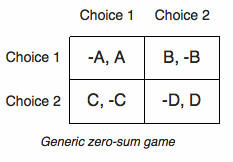
完全な情報が与えられるゲームの純粋戦略による解は、一般的な場合による確率化の必要性との 対照により、はじめて重要性をもつ。
「ミニマックス定理は、フォン・ノイマンが生産の線 形モデル(linear model)の解析にむかったときに新しい装い」をもつ。
「ブラウワーの不動点定
理」の拡張にはじまり……
ナッシュ均衡(Nash equilibrium)
ゲームに参加するすべてのプレイヤーが相互に他者の
戦略を考慮に入れて、自己の利益を最大にする均衡状態。
+++
ゲーム理論を、健康行動の分野で解析・応用しようと
するのが、行動ゲーム理論(behavioral
game theory)である。
+++
リンク
文献
++++
Copyright Mitzub'ixi Quq Chi'j, 2015




