アンドロイド(Android) は現場力を発揮することができるか？　この疑問に私が答えるとす れば、それは「否」である。あるいは現場力を身につけたアンドロイドは、もはや、そうだ とは定義できず「新人類」なのである。こ の思考実験とそれに対する私の応答は「ロボットに演出をつける」という荒唐無稽なプロジェクトへの揶揄ではない。ロボット演劇チームの狙いは、この問いへ の技術的応答にあるのではなく、この試みを通した技術と演劇の予期せぬ創発的な展開を引き出すことであり、ここでの私の態度は偽悪漢ぶっているだけであ る。かくのごとく、現場力は人間の定義にまで及ぶ重要な属性であることを論証しようというのが私の狙いである。

私は現場力が発揮された場所において、（定義変更の前のアンドロイドを含む） 行為者たちとその周囲にみられる抽象的属性を次の５つに分けた。１）場所性・状況性、２）意識性、３）物理性・道具性、４）媒介性、５）身体性である。私 は現場力を、個人や集団が「所有」できる技能や能力ではなく、場所依存した行為者の能力の顕現であり、身体が深く関わるコミュニケーションの延長に位置づ けられるために「きわめて社会的な概念」であると述べた［池田 Online］。

私は過度の人間中心主義者ではないが、実験状況において高度に組織化された実験統制状況におかれた一部の高等霊長類を除けば、人間は、行為や意 識の中に未来の時間的要素を組み込める高度で複雑な情報処理をおこない、さらにそれを言語により外部表象化できる——つまり個体間で正確な情報伝達とその 蓄積が可能な——ほとんど唯一の動物であると考える。いやいや集団で狩りをするチンパンジーも臨機応変な現場力をもっているではないという反論があるかも しれない。だが、件の動物は上記の３）に属する狩猟道具を使うことができない点で失格である。近年の発掘成果によると北米最古の先史考古文化のクロービス 人（紀元前１万３千〜８千５百年前）は、効率的な狩猟道具の発明によって大型ほ乳類の大量虐殺と絶滅という人類の「はじめての原罪」という不名誉をほしい ままにしている。現場力をはじめて身に付けたアンドロイドは、その見事なしぐさによって人間の魂を打ち震わすだけではなく、アンドロイドに仕事を押し付け る人間に反感をもち、人間にとっては都合の悪い現場力をつける可能性がある。そのために も、この問いの答えは「否」であってほしいのだ。

アンドロイド（androido）の語義

OED 定義は、An automaton resembling a human beingだそうです。なんと初出は、1727–51 Chambers Cycl. s.v., Albertus Magnus is recorded as having made a famous androides. 従って、オーギュスト・ヴィリエ・ド・リラダン（Jean-Marie-Mathias-Philippe-Auguste, comte de Villiers de l'Isle-Adam, 1838-1889）が、『未来のイヴ』において、初めて「アンドロイド（Andréide）」という呼称を用いたというのも（Wiki日本語）信憑性に 信頼性がおけるわけではないようだ。英語では1795年の『ロ ンドンタイムス』Early example of the term androides used to describe human-like mechanical devices, London Times, 22 December 1795に登場している

"The Oxford English Dictionary traces the earliest use (as "Androides") to Ephraim Chambers' 1728 Cyclopaedia, in reference to an automaton that St. Albertus Magnus allegedly created.[3][8] By the late 1700s, "androides", elaborate mechanical devices resembling humans performing human activities, were displayed in exhibit halls.[9] The term "android" appears in US patents as early as 1863 in reference to miniature human-like toy automatons.[10] The term android was used in a more modern sense by the French author Auguste Villiers de l'Isle-Adam in his work Tomorrow's Eve (1886).[3] This story features an artificial humanlike robot named Hadaly. As said by the officer in the story, "In this age of Realien advancement, who knows what goes on in the mind of those responsible for these mechanical dolls." The term made an impact into English pulp science fiction starting from Jack Williamson's The Cometeers (1936) and the distinction between mechanical robots and fleshy androids was popularized by Edmond Hamilton's Captain Future stories (1940–1944).[3]"

オックスフォード・イングリッシュ・ディクショナリーでは、聖アルベルトゥス・マグナスが制作したとされるオートマトンを指して、エフライム・ チェンバースの1728年のCyclopaediaに "Androides "として使われたのが最初とされている。1700年代後半には、人間の活動を模した精巧な機械装置である「アンドロイド」が展示場に展示されていた。アン ドロイド」という言葉は、1863年にはアメリカの特許に登場しており、人間のようなミニチュアのおもちゃのオートマトンを指していた。アンドロイドとい う言葉をより現代的な意味で使ったのは、フランスの作家オーギュスト・ヴィリエ・ド・リル・アダムの『明日のイヴ』（1886年）という作品である。この 作品には、ハダリーという人造人間のようなロボットが登場する。物語の中で将校が言ったように、"このリアリエンの進歩の時代に、この機械人形の責任者の 心の中がどうなっているのか、誰にもわからない "のである。この言葉は、ジャック・ウィリアムソンの『The Cometeers』（1936年）から始まる英国のパルプSFに影響を与え、機械的なロボットと肉的なアンドロイドの区別は、エドモンド・ハミルトンの 『キャプテン・フューチャー』（1940-1944年）の物語で広まった（ https://www.deepl.com/ja/translator で翻訳）。

●アンドロイド、またわ、人造人間

「假にひとつの單獨な語……《もうすでに!》といふ言葉が、——或る瞬間、——「人造人間」の言ふべき言葉だとしますよ」——ヴィリエ・ド・リ ラダン『未來のイヴ』齋藤磯雄譯、p272、東京創元社、1996年

★オートマトン

+++

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton (automata in plural) is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states (represented in the figure by circles) and transitions (represented by arrows). As the automaton sees a symbol of input, it makes a transition (or jump) to another state, according to its transition function, which takes the previous state and current input symbol as its arguments. Automata theory is closely related to formal language theory. In this context, automata are used as finite representations of formal languages that may be infinite. Automata are often classified by the class of formal languages they can recognize, as in the Chomsky hierarchy, which describes a nesting relationship between major classes of automata. Automata play a major role in the theory of computation, compiler construction, artificial intelligence, parsing and formal verification.	オートマトン理論とは、抽象的な機械やオートマトン、またそれらを用い て解くことのできる計算問題を研究する学問である。数理論理学と密接な関係を持つ理論計算機科学の理論である。オートマトンの語源はギリシャ語の αὐτόματοςであり、「自己作用、自己意志、自己運動」を意味する。オートマトン（複数形はオートマタ）は、あらかじめ決められた一連の動作に自動 的に従う、抽象的な自走式計算装置である。有限個の状態を持つオートマトンは、有限オートマトン（FA）または有限状態機械（FSM）と呼ばれる。右の図 は有限状態機械を示しており、オートマトンの一種としてよく知られている。このオートマトンは、状態（図では丸で表現）と遷移（矢印で表現）からなる。 オートマトンは入力記号を見ると、前の状態と現在の入力記号を引数とする遷移関数に従って、別の状態への遷移（またはジャンプ）を行う。 オートマトン理論は、形式言語理論と密接に関連している。この文脈では、オートマトンは無限である可能性のある形式言語の有限表現として用いられる。オー トマトンはしばしば、オートマトンの主要なクラス間の入れ子関係を記述するチョムスキー階層にあるように、認識できる形式言語のクラスによって分類され る。オートマトンは、計算理論、コンパイラ構築、人工知能、構文解析、形式検証において重要な役割を果たしている。
Classes of automata (Clicking on each layer gets an article on that subject)	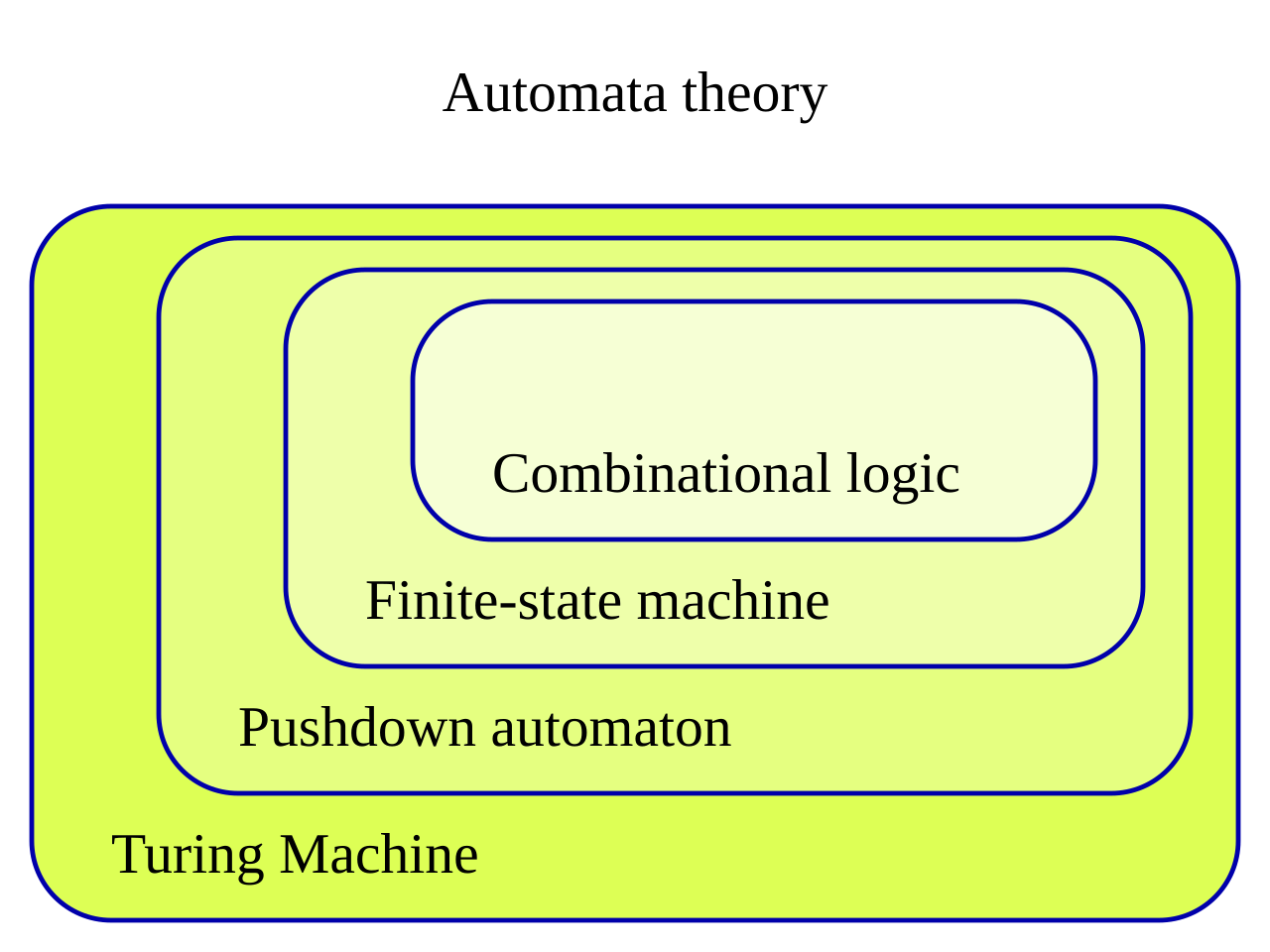オートマトンのクラス (各層をクリックすると、そのテーマに関する記事が表示される）
In automata theory, combinational logic (also referred to as time-independent logic[1]) is a type of digital logic that is implemented by Boolean circuits, where the output is a pure function of the present input only. This is in contrast to sequential logic, in which the output depends not only on the present input but also on the history of the input. In other words, sequential logic has memory while combinational logic does not. Combinational logic is used in computer circuits to perform Boolean algebra on input signals and on stored data. Practical computer circuits normally contain a mixture of combinational and sequential logic. For example, the part of an arithmetic logic unit, or ALU, that does mathematical calculations is constructed using combinational logic. Other circuits used in computers, such as half adders, full adders, half subtractors, full subtractors, multiplexers, demultiplexers, encoders and decoders are also made by using combinational logic. Practical design of combinational logic systems may require consideration of the finite time required for practical logical elements to react to changes in their inputs. Where an output is the result of the combination of several different paths with differing numbers of switching elements, the output may momentarily change state before settling at the final state, as the changes propagate along different paths. [2]	オートマトン理論では、組み合わせ論理（時間非依存論理[1]とも呼ば れる）はブール回路で実装されるデジタル論理の一種であり、出力は現在の入力のみの純粋関数である。これは、出力が現在の入力だけでなく、入力の履歴にも 依存する逐次論理とは対照的である。言い換えれば、逐次論理にはメモリがあるが、組合せ論理にはない。 組合せ論理は、コンピュータ回路において、入力信号および記憶されたデータに対してブール代数を実行するために使用される。実用的なコンピュータ回路に は、通常、組合せ論理と逐次論理が混在している。例えば、算術論理演算装置（ALU）のうち、数学的計算を行う部分は組合せ論理で構成されている。その 他、半加算器、全加算器、半減算器、全減算器、マルチプレクサ、デマルチプレクサ、エンコーダ、デコーダなど、コンピュータで使われる回路も組み合わせ論 理で作られている。 組合せ論理システムの実用的な設計には、実用的な論理素子が入力の変化に反応するのに必要な有限時間を考慮する必要があるかもしれない。出力が、スイッチ ング素子の数が異なる複数の異なる経路の組み合わせの結果である場合、出力は、変化が異なる経路に沿って伝播するため、最終的な状態に落ち着く前に瞬間的 に状態が変化する可能性がある。[2]
A finite-state machine (FSM) or finite-state automaton (FSA, plural: automata), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition.[1] An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines.[2] For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are: vending machines, which dispense products when the proper combination of coins is deposited; elevators, whose sequence of stops is determined by the floors requested by riders; traffic lights, which change sequence when cars are waiting; combination locks, which require the input of a sequence of numbers in the proper order. The finite-state machine has less computational power than some other models of computation such as the Turing machine.[3] The computational power distinction means there are computational tasks that a Turing machine can do but an FSM cannot. This is because an FSM's memory is limited by the number of states it has. A finite-state machine has the same computational power as a Turing machine that is restricted such that its head may only perform "read" operations, and always has to move from left to right. FSMs are studied in the more general field of automata theory.	有限状態機械（FSM）または有限状態オートマトン（FSA、複数形は オートマトン）、有限オートマトン、または単に状態機械は、計算の数学的モデルである。FSMは、任意の時点で有限個の状態のうちの1つになることができ る抽象的な機械である。FSMは、ある入力に応答して、ある状態から別の状態に変化することができる。ある状態から別の状態への変化は遷移と呼ばれる。有 限状態マシンには、決定論的有限状態マシンと非決定論的有限状態マシンの2種類がある。 ステートマシンのパフォーマティビティは、現代社会の多くの装置で観察することができ、それらは、提示されたイベントのシーケンスに応じて、予め決められ た一連の動作を実行する。簡単な例としては、適切な硬貨の組み合わせが投入されると商品が払い出される自動販売機、乗車客が要求した階によって停止順序が 決まるエレベーター、車が待機していると順序が変わる信号機、適切な順序の数字列の入力を必要とするコンビネーション・ロックなどがある。 有限状態機械は、チューリング機械などの他の計算モデルよりも計算能力が低い[3]。計算能力の違いは、チューリング機械にはできるが、FSMにはできな い計算タスクがあることを意味する。これは、FSMのメモリが状態の数によって制限されるためである。有限状態機械は、チューリング機械と同じ計算能力を 持つが、その頭部は「読み取り」操作しか行えず、常に左から右に移動しなければならないという制約がある。FSMは、より一般的なオートマトン理論の分野 で研究されている。
In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack. Pushdown automata are used in theories about what can be computed by machines. They are more capable than finite-state machines but less capable than Turing machines (see below). Deterministic pushdown automata can recognize all deterministic context-free languages while nondeterministic ones can recognize all context-free languages, with the former often used in parser design. The term "pushdown" refers to the fact that the stack can be regarded as being "pushed down" like a tray dispenser at a cafeteria, since the operations never work on elements other than the top element. A stack automaton, by contrast, does allow access to and operations on deeper elements. Stack automata can recognize a strictly larger set of languages than pushdown automata.[1] A nested stack automaton allows full access, and also allows stacked values to be entire sub-stacks rather than just single finite symbols.	理論計算機科学の一分野である計算理論において、プッシュダウン・オートマトン（PDA）はスタックを用いたオートマトンの一種である。 プッシュダウン・オートマトンは、機械が何を計算できるかという理論に使われる。有限状態機械よりは高性能だが、チューリング機械（後述）よりは性能が劣 る。決定論的プッシュダウン・オートマトンはすべての決定論的文脈自由言語を認識することができ、非決定論的プッシュダウン・オートマトンはすべての文脈 自由言語を認識することができる。 プッシュダウン」とは、スタックが、カフェテリアのトレー・ディスペンサーのように「押し下げられる」とみなすことができることを意味する。対照的に、ス タック・オートマトンは、より深い要素へのアクセスと操作を可能にする。スタック・オートマトンは、プッシュダウン・オートマトンよりも厳密に大きな言語 集合を認識することができる[1]。ネストされたスタック・オートマトンは、完全なアクセスを可能にし、また、スタックされた値を単一の有限記号ではな く、サブスタック全体にすることができる。
A Turing machine is a mathematical model of computation describing an abstract machine[1] that manipulates symbols on a strip of tape according to a table of rules.[2] Despite the model's simplicity, it is capable of implementing any computer algorithm.[3] The machine operates on an infinite[4] memory tape divided into discrete cells,[5] each of which can hold a single symbol drawn from a finite set of symbols called the alphabet of the machine. It has a "head" that, at any point in the machine's operation, is positioned over one of these cells, and a "state" selected from a finite set of states. At each step of its operation, the head reads the symbol in its cell. Then, based on the symbol and the machine's own present state, the machine writes a symbol into the same cell, and moves the head one step to the left or the right,[6] or halts the computation. The choice of which replacement symbol to write, which direction to move the head, and whether to halt is based on a finite table that specifies what to do for each combination of the current state and the symbol that is read. Like a real computer program, it is possible for a Turing machine to go into an infinite loop which will never halt. The Turing machine was invented in 1936 by Alan Turing,[7][8] who called it an "a-machine" (automatic machine).[9] It was Turing's doctoral advisor, Alonzo Church, who later coined the term "Turing machine" in a review.[10] With this model, Turing was able to answer two questions in the negative: Does a machine exist that can determine whether any arbitrary machine on its tape is "circular" (e.g., freezes, or fails to continue its computational task)? Does a machine exist that can determine whether any arbitrary machine on its tape ever prints a given symbol?[11][12] Thus by providing a mathematical description of a very simple device capable of arbitrary computations, he was able to prove properties of computation in general—and in particular, the uncomputability of the Entscheidungsproblem ('decision problem').[13] Turing machines proved the existence of fundamental limitations on the power of mechanical computation.[14] While they can express arbitrary computations, their minimalist design makes them too slow for computation in practice: real-world computers are based on different designs that, unlike Turing machines, use random-access memory. Turing completeness is the ability for a computational model or a system of instructions to simulate a Turing machine. A programming language that is Turing complete is theoretically capable of expressing all tasks accomplishable by computers; nearly all programming languages are Turing complete if the limitations of finite memory are ignored.	チューリング機械は、抽象的な機械[1]を記述する計算の数学的モデルであり、規則表に従ってテープ片上の記号を操作する[2]。このモデルは単純であるにもかかわらず、あらゆるコンピュータアルゴリズムを実装することができる[3]。 マシンは、離散的なセル[5]に分割された無限[4]のメモリテープ上で動作し、各セルは、マシンのアルファベットと呼ばれる記号の有限集合から引き出さ れた単一の記号を保持することができる。マシンの動作のどの時点でも、これらのセルの1つの上に配置される「ヘッド」と、有限の状態セットから選択される 「状態」を持つ。動作の各段階で、ヘッドはそのセルのシンボルを読み取る。次に、その記号とマシン自身の現在の状態に基づいて、マシンは同じセルに記号を 書き込み、ヘッドを左または右に1ステップ動かすか[6]、計算を停止する。どの置換記号を書き込むか、ヘッドをどの方向に動かすか、そして停止す るかどうかの選択は、現在の状態と読み込まれた記号の組み合わせごとに何をす べきか規定した有限表に基づいている。実際のコンピュータ・プログラムのように、チューリング・マシンが無限ループに入ることは可能であり、決して停止す ることはない。 チューリング機械は1936年にアラン・チューリングによって発明され[7][8]、彼はこれを「a-machine」（自動機械）と呼んだ[9]。 チューリングの博士課程の指導教官であったアロンゾ・チャーチが、後にレビューの中で「チューリング機械」という言葉を作った[10]： テープ上の任意の機械が「循環」（例えば、フリーズしたり、計算タスクを継続できなかったり）するかどうかを決定できる機械は存在するか？ テープ上の任意の機械が、与えられた記号を印刷したことがあるかどうかを決定できる機械は存在するか[11][12]。 こうしてチューリングは、任意の計算が可能な非常に単純な装置の数学的記述を提供することによって、一般的な計算の特性、特にEntscheidungsproblem（「決定問題」）の計算不可能性を証明することができた[13]。 チューリング機械は任意の計算を表現することができるが、そのミニマリスト的な設計のため、実際の計算には遅すぎる。 チューリング完全性とは、計算モデルや命令体系がチューリング機械をシミュレートする能力のことである。チューリング完全性を持つプログラミング言語は、 理論的にはコンピュータが達成可能なすべてのタスクを表現できる。有限メモリの制約を無視すれば、ほぼすべてのプログラミング言語はチューリング完全性を 持つ。
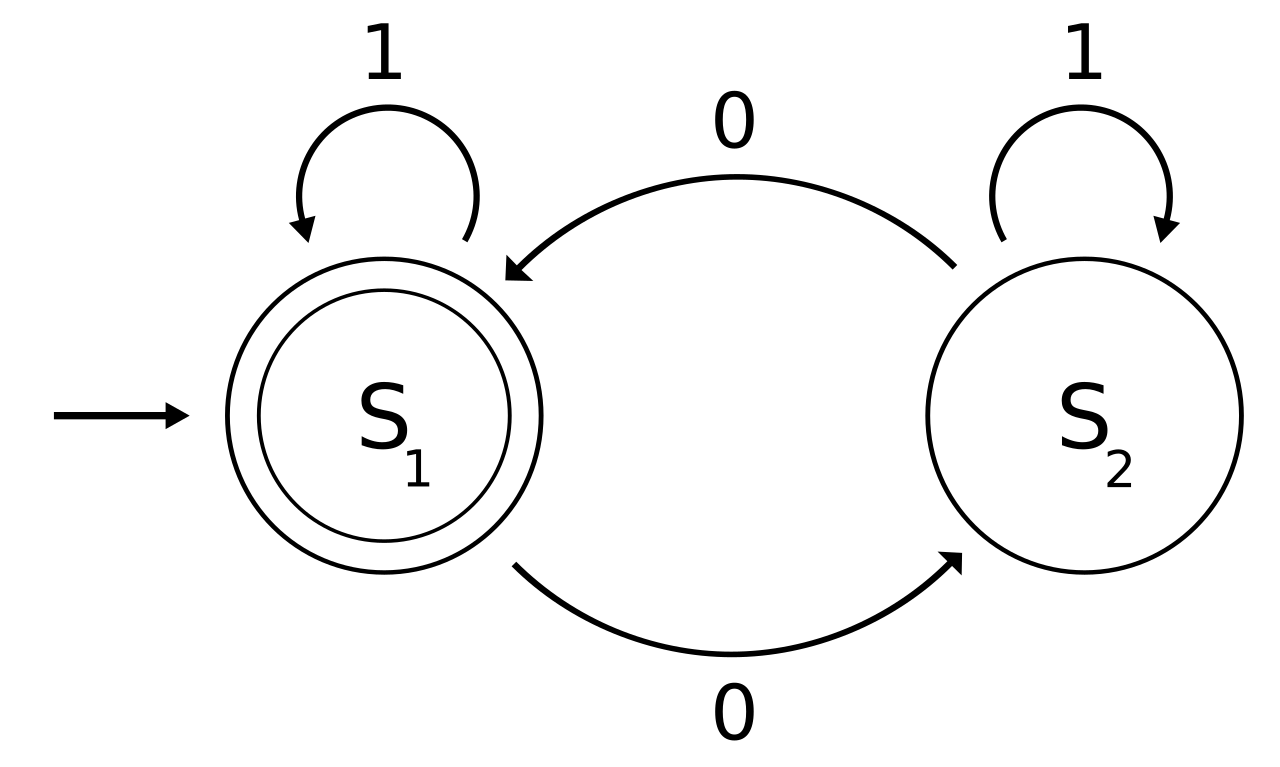The automaton described by this state diagram starts in state S1, and changes states following the arrows marked 0 or 1 according to the input symbols as they arrive. The double circle marks S1 as an accepting state. Since all paths from S1 to itself contain an even number of arrows marked 0, this automaton accepts strings containing even numbers of 0s.	この状態図で記述されるオートマトンは状態S1から始まり、入力記号の到着に従って0または1と書かれた矢印に従って状態を変化させる。二重丸はS1が受 け入れ状態であることを示す。S1からそれ自身へのすべての経路は偶数の0と書かれた矢印を含むので、このオートマトンは偶数の0を含む文字列を受け入れ る。
https://en.wikipedia.org/wiki/Automata_theory

+++++

リンク

文献

初出誌 141）「アンドロイドは現場力を発揮することができるか？」『Communication-Design 5』p.86、大阪大学コミュニケーションデザイン・センター、2011年9月（→池田業績）